Bonjour ,
Montrer pour tout k∈N* 1/(2k) ≤ √k- √(k-1)
Deduire que pour tout n ∈N*
Σ (de k=1 à n )(1/k) ≤ 2√n.
Suite réelle
5 messages
- Page 1 sur 1
Re: Suite réelle
Bonjour
Qu'as-tu fait, cherché ?
1) Utiliser la quantité conjuguée de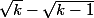 puis majorer
puis majorer 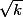
2) Ecrire les n termes de la somme télescopique des inégalités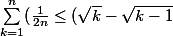))
Qu'as-tu fait, cherché ?
1) Utiliser la quantité conjuguée de
2) Ecrire les n termes de la somme télescopique des inégalités
Re: Suite réelle
Je n arrive pas à faire la somme télescopique
Pourqoi tu as écrit Σ ( 1/2n) pas Σ (1/ 2k) ??
Pourqoi tu as écrit Σ ( 1/2n) pas Σ (1/ 2k) ??
Re: Suite réelle
oui, erreur de frappe
On sort le 1/2 de la somme :
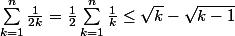
Ecris les n inégalités pour k =1 à n et ajoute les terme à terme. Qu'est-ce que tu constates ?
On sort le 1/2 de la somme :
Ecris les n inégalités pour k =1 à n et ajoute les terme à terme. Qu'est-ce que tu constates ?
Re: Suite réelle
Σ 1/(2k)< 1-0+ ..+√n+√(n-1) qui s éliminant membre à membre
D où Σ 1/k < 2√n
Merci beaucoup pour ton aide .
D où Σ 1/k < 2√n
Merci beaucoup pour ton aide .
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
