Récurrence suite réelle

[Sawamura07]

Bonjour à tous
J'ai un petit exercice de suite à faire et je me sens un peu perdu
On a


Montrer que pour tout n * :


Je pense que cela se résout avec le principe de récurrence
En prenant n=1 et en faisant les calculs des deux cotés j'ai trouvé l'égalité => vrai
Maintenant en supposant que
est vraie et en essayent de montrer que je me bloque en faisant les calculs j'y arrive pas //
Merci d'avance

[capitaine nuggets]

Bonjour à tous
J'ai un petit exercice de suite à faire et je me sens un peu perdu
On a


Montrer que pour tout n * :

Dans ton énoncé, au début, ne serait-ce pas plutôt ?

D'après cette hypothèse

Ensuite, fais intervenir la quantité conjuguée de :

[CENTER][/CENTER]

Développe le numérateur et tu auras ce que tu veux :+++:

Remarque : je ne sais pas si cette question est posée dans l'exercice, mais il faudrait montrer que la suite vérifie , car sinon la suite ne sera plus définie à partir d'un certain rang.

[Sawamura07]

Oui effectivement c'est
Non ça n'a pas été posé , et 'apres l'énoncé on nous dit que la suite est définie sur N
Merci pour ton aide

[capitaine nuggets]

Oui effectivement c'est
Non ça n'a pas été posé , et 'apres l'énoncé on nous dit que la suite est définie sur N
Merci pour ton aide

Oui, oui, je sais pas pourquoi j'ai rajouté une étoile :crash:

Alors concernant le fait que soit bien définie, je dirais que normalement, une question devrait être posée pour justifié ces calculs. En effet, dans l'énoncé et même dans l'expression qu'on te demande de montrer, sans étude préalable, à priori rien n'empêcherai d'obtenir un terme de la suite qui contiendrait une racine d'un réel strictement négatif.
Donc, si on voulait bien faire les choses, il faudrait avant tout calcul, montrer par récurrence que tout se passe bien pour la suite , c'est-à-dire quel que soit , .
(après ça dépend de ce que tu as vu...).

:+++:

[Sawamura07]

Ah oui je comprends maintenant
Sinon je me suis encore bloqué à un exercice du même genre . On vient de voir le principe de récurrence en classe et je suis pas trop à l'aise avec x)
J'espere que vous pourrez m'aider
n appartient à N*

Démontrer par récurrence que

[capitaine nuggets]

Ah oui je comprends maintenant
Sinon je me suis encore bloqué à un exercice du même genre . On vient de voir le principe de récurrence en classe et je suis pas trop à l'aise avec x)
J'espere que vous pourrez m'aider
n appartient à N*

Démontrer par récurrence que

Salut !

Qu'est-ce que ?

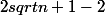
[Sawamura07]

je m'excuse j'ai oublié de le préciser
c'est la somme que j'ai déjà donnée

[Shew]

Ah oui je comprends maintenant
Sinon je me suis encore bloqué à un exercice du même genre . On vient de voir le principe de récurrence en classe et je suis pas trop à l'aise avec x)
J'espere que vous pourrez m'aider
n appartient à N*

Démontrer par récurrence que

On vérifie dans un premier temps et pour . Puis, en partant du principe que la proposition est vraie au rang n, on vérifie le rang n + 1 . Pour la somme on développe

[capitaine nuggets]

Ah oui je comprends maintenant
Sinon je me suis encore bloqué à un exercice du même genre . On vient de voir le principe de récurrence en classe et je suis pas trop à l'aise avec x)
J'espere que vous pourrez m'aider
n appartient à N*

Démontrer par récurrence que

je m'excuse j'ai oublié de le préciser
c'est la somme que j'ai déjà donnée

Initialisation : Montre que l'inégalité est vraie pour le premier indice , c'est-à-dire montre que .
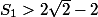
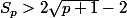
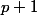
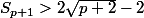
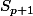
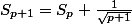
Hérédité : Suppose que l'inégalité que tu veux montrer est vraie pour un certain indice , c'est-à-dire suppose que , montre qu'alors pour l'indice suivant , on a . Pour montrer cette dernière inégalité, pars de en remarquant que , puis utilise l'inégalité de l'hypothèse de récurrence. :+++:

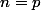
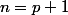
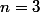
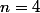
Interprétation du raisonnement : L'inégalité est vraie pour , et comme on montre que si on suppose que l'inégalité obtenue pour est vraie, l'inégalité obtenue pour est aussi vraie, on en déduit qu'à partir de l'inégalité , l'inégalité suivante obtenue pour est aussi vraie, l'inégalité obtenue pour est vraie, l'inégalité obtenue pour est vraie et ainsi de suite..., donc au final l'inégalité est vraie pour tout :++:
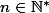