Bonjour ,
Pouvez vous m aider à faire cette question concernant les suites réelles ?
Un= Σ(de k=0 à 2n+1) (n/(n^2+k))
On a 2-2/(n+1)《Un《2+2/n
Deduire que Un est convergente
Merci d avance
Suite réelle
11 messages
- Page 1 sur 1
Re: Suite réelle
Tu écris on a.
L'as-tu démontré ou est-ce admis ?
Les 2n+1 premiers termes en partant de la droite sont majorés par
en rajoutant
soit
Les 2n+1 premiers termes en partant de la gauche sont minorés par
En rajoutant
Puis un peu de cuisine :
EDIT
C'est affreux chaque fois que je corrige mon texte, une phrase parasite s'insère à un autre endroit.
C'est comme si ma souris ou mon clavier bégayait .
Je renonce !!!
Oui c'était vraiment le bazar, j'ai corrigé
Re: Suite réelle
Par contre Carpate, je ne vois pas pourquoi tu t'embêtes à séparer les termes.
On a pour tout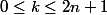
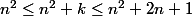
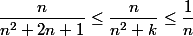
En sommant de k=0 à 2n+1
}{(n+1)^2} \leq u_n \leq \dfrac{2n+2}{n})
etc ...
On a pour tout
En sommant de k=0 à 2n+1
etc ...
Re: Suite réelle
Ma question c est comment on démontre que Un est monotone en utilisant cette inégalité
Est elle croissante ou décroissante ?
Est elle croissante ou décroissante ?
Re: Suite réelle
D aprés le théorèmes de convergence : une suite croissante et majorée est convergente
Une suite décroissante et minorée est convergente
Et la question :montrer que Un est convergente ça revient a démontrer qu elle est monotone ?
Une suite décroissante et minorée est convergente
Et la question :montrer que Un est convergente ça revient a démontrer qu elle est monotone ?
Re: Suite réelle
Et le théorème des gendarmes ?
Sa Majesté a écrit:Quelle est la limite en l'infini de?
Quelle est la limite en l'infini de?
Re: Suite réelle
Bon il faut 10 messages dans ce fil pour que tu postes enfin l'énoncé.
Et comme je m'y attendais et contrairement à ce que tu as affirmé, on ne te demande pas de montrer la monotonie de U, mais simplement de montrer qu'elle est convergente.
Donc je redis : théorème des gendarmes.
Et comme je m'y attendais et contrairement à ce que tu as affirmé, on ne te demande pas de montrer la monotonie de U, mais simplement de montrer qu'elle est convergente.
Donc je redis : théorème des gendarmes.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
