Suite récurrente

[papacal]

Bonjour,
Je coince sur une demo. La question est la suivante
Soit une suite Un définie par Uo=1 et
U(n+1)=Un + n/6 (n^2 - 3n + 8)
Démontrer que Un=2^(n-1)

J'ai bien essayé la division de deux termes consécutifs et autres additions mais je ne tombe que sur des équations impossibles à expliquer à un élève de 1ere .
Toute aide me sera d'un grand secours.

[Tiruxa47]

Bonjour,
L'énoncé me semble faux,
Si on calcule les premiers termes, on trouve
1, 2, 4, 8, 16
c'est bon donc jusqu'à U(5)
mais pour U(6)
U(5+1)=U(5)+(5/6)(25-15+8)=U(5)+15=31
alors que la formule donnerait 2^5 soit 32
et en continuant....
La formule n'est valable que pour n compris entre 1 et 5.
Mais on pouvait s'en douter car cela signifierait que U(n) est géométrique donc que U(n+1)-U(n) est géométrique ainsi définie par une fonction exponentielle
Or ici U(n+1)-U(n) est un polynôme du troisième degré, soit une fonction qui n'a pas la même vitesse de croissance qu'une exponentielle.

[chan79]

salut
on additionne membre à membre les
après un peu de calcul on trouve

[Ben314]

Salut,
Voire même, partant de (coeff. binomiaux "étendus" qui sont bien plus facile à sommer que les 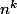) on trouve immédiatement
Qui, en plus, dit aussi que lorsque 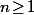(et ), ce qui a le bon gout d'expliquer pourquoi lorsque

[pascal16]

Variante :
U(n+1)-Un = n/6 (n^2 - 3n + 8)
si Un+1 vaut 2^n, on a Un+1-Un= 2^n-2^(n-1)=2^(n-1)

soit n/6 (n^2 - 3n + 8)=2^(n-1)

de part les croissances comparées de x-> x^3 et x-> 2^x, le second terme croit bcp plus vite quand n augmente, il ne peuvent être égaux pour toute valeur de n, l'affirmation (assertion) de départ est donc fausse.

[papacal]

Rebonjour
Merci à tous pour vos réponses pointues, j'avais compris que quelque chose d'évident m'échappait mais je ne savais pas quoi.
Je me félicite de m'être adressé à vous. Bonne soirée et bon week end à tous les matheux.