Ce n'est pas une somme mais un produit :nxthunder a écrit:
ET je voudrais savoir comment pourrais t-on l'écrire avec le
Suite de polynome
26 messages
- Page 2 sur 2 - 1, 2
par rene38 » 18 Sep 2006, 16:54
par nxthunder » 18 Sep 2006, 18:30
Si je sors ca a mon prof, il va faire une sacrée tete je suis qu'en terminale hein :we:
Sinon pour
C'est bon Nox ?
Sinon pour
par nox » 19 Sep 2006, 08:25
Un peu tard mais bon ^^
Donc non pour Qn+1 ca n'a pas l'air d'être ça.
Déja pour Qn
je dirai plutot
\times.....\times(x+n-1))
Ce qui donnerai
})
et donc
})
tout simplement
Donc non pour Qn+1 ca n'a pas l'air d'être ça.
Déja pour Qn
nxthunder a écrit:
je dirai plutot
Ce qui donnerai
et donc
par nxthunder » 19 Sep 2006, 20:46
LE raisonnement par récurrence suivant est-il juste ?
Notons les hypothèses :
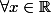
on a =1)
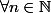
et
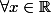
On a)
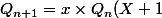1 ) Déterminons)
, )
et )
Pour :
= =x\times Q_0(X+1))
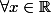
Or on a
Alors on peut écrire que=x\times 1 = x)
Pour :
= =x\times Q_1(X+1))
=x\times (X+1))
Pour :
= =x\times Q_2(X+1))
=x\times (x+1)\times(x+1+1))
=x\times (X+1)\times(X+2))
2 ) Conjecturons une écriture de)
:
Pour :
=x\times (X+1)\times(X+2)\times.....\times(X+n-1))
ou encore = \prod_{i=1}^{n-1} (x+i))
3 ) Démontrons cette conjecture :
Je note P(n) la propriété telle que
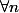
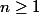
on a P(n) =
Initialisation : Calculons P(1)
Posons :
=Q_n(X))
et =\prod_{i=1}^{n-1} (x+i))
=Q_1(X)=x)
= \prod_{i=1}^{1-1} (x+0)=x\times 1 = x)
Donc=u_n(X))
Ainsi P(1) est vraie.
Hérédité : Soit
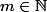
tel que P(m) soie vraie.
Montrons qu'alors P(m+1) est vraie, c'est à dire que=x\times (X+1)\times.....\times(X+n))
Par hyp on a :
=\prod_{i=1}^{m-1} (x+i))
et=x\times Q_n(X+1))
=x\times (X+1)\times(X+2)\times.....\times(X+n-1))
=(x+1)\times (X+2)\times(X+3)\times.....\times(X+n))
=x\times (x+1)\times (X+2)\times(X+3)\times.....\times(X+n))
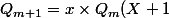=x\times (x+1)\times (X+2)\times(X+3)\times.....\times(X+n))
Bilan : P(m) implique P(m+1)
Conclusion : P(n) est vraie.
========================
Une petite question ? Est ce que)
)
= )
..????
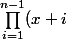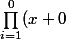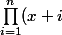Sinon cest pas i=0 car pour)
il y aurait du "x" dedans. Or
Notons les hypothèses :
On a
1 ) Déterminons
Pour
Or
Alors on peut écrire que
Pour
Pour
2 ) Conjecturons une écriture de
Pour
ou encore
3 ) Démontrons cette conjecture :
Je note P(n) la propriété telle que
Initialisation : Calculons P(1)
Posons :
Donc
Ainsi P(1) est vraie.
Hérédité : Soit
Montrons qu'alors P(m+1) est vraie, c'est à dire que
Par hyp on a :
et
Bilan : P(m) implique P(m+1)
Conclusion : P(n) est vraie.
========================
Une petite question ? Est ce que
Sinon cest pas i=0 car pour
26 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :