Suite geometrique - 1S

[Combattant204]

Bonsoir tout le monde,
Je bloque un peu dans ces petits exercices et j'ai besoin qu'on m'affirme si ce que je suis entrain de faire est juste.
1.(Vn) est une suite geometrique de premier terme V0 et de raison q telle que V2 = -18 et V4 = -162.
Determiner q et V0.
2.Calculer la somme S = 4 + 2 + 1 + 1/2 + ... + 1/32768
3.Calculer la somme S = 1/3 - 1/9 + 1/27 - ... - 1/6561

Mes reponses
1-Vn etant une suite geometrique,on peut employer la formule:Vn = Up.q^(n-p)
On determine d'abord q,soit:
V4 = V2.q^(4-2)
<=> -162 = -18.q^2
<=> q^2 = 82/9
<=> q = V82/3
Soit encore V0 = V2.q^(0-2)
<=>V0 = -18.(V82/3)^-2
<=> V0 = -162/83

2.je sais que la raison est 0,5 et que je dois utiliser la formule
1er terme . (1-q^nombre de termes)/(1 - q)
Mais je ne connais pas le nombre de termes,comment faire pour le determiner?

3.Y'a-t-il une erreur dans cet exercice?
Il y'a une fois + et une fois - , comment suis-je suppose calculer cet somme au-juste? :hein: :hein:

De l'aide s'il vous plait!

[Sylviel]

Que vaut 162 /2 ? :zen:

[Combattant204]

Que vaut 162 /2 ? :zen:

Merci pour votre reponse!
Oui je vois que j'ai fait une erreur de calcul dans la 1.
-162 = -18.q^2
q^2 = 9
q = 3
Et V0 = -18(3)^-2
V0 = - 2

Est ce juste cette fois? Et comment faire pour le reste?
162/2 = 81 mais ne vouliez vous pas dire 162/18?

[capitaine nuggets]

Salut !

2.Calculer la somme S = 4 + 2 + 1 + 1/2 + ... + 1/32768

2.je sais que la raison est 0,5 et que je dois utiliser la formule
1er terme . (1-q^nombre de termes)/(1 - q)
Mais je ne connais pas le nombre de termes,comment faire pour le determiner?

2. est la somme de termes consécutifs ( sera à préciser) d'une suite géométrique de premier terme et de raison 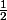, mais on peut également le voir comme la somme de termes consécutifs d'une suite géométrique de premier terme et de raison .

Après, suivant les deux considérations que je t'ai donnée, tu peux transformer de telle manière que le premier terme soit et la raison soit respectivement 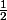ou , il sera alors plus simple de déterminer le nombre de termes. En factorisant par , ou par , peut s'exprimer de deux façons :

[CENTER]

ou encore
[/CENTER]

Pour trouver le nombre de termes , il suffira de trouver l'entier respectivement tel que :

[CENTER]

ou encore [/CENTER]

[Combattant204]

Salut !



2. est la somme de termes consécutifs ( sera à préciser) d'une suite géométrique de premier terme et de raison , mais on peut également le voir comme la somme de termes consécutifs d'une suite géométrique de premier terme et de raison .
(Es-tu sûr qu'il s'agit de 6561 ? Ca me paraît bizarre, c'est pas une puissance de 2...).

Après, suivant les deux considérations que je t'ai donnée, tu peux transformer de telle manière que le premier terme soit et la raison soit respectivement ou , il sera alors plus simple de déterminer le nombre de termes. En factorisant par , ou par , peut s'exprimer de deux façons :

[CENTER]

ou encore
[/CENTER]

Pour trouver le nombre de termes , il suffira de trouver l'entier respectivement tel que :

[CENTER]

ou encore [/CENTER]

Pardon capitainenuggets,c'est ma faute,en effet le dernier terme est 1/32768!

[capitaine nuggets]

Pardon capitainenuggets,c'est ma faute,en effet le dernier terme est 1/32768!

Ca y est, j'ai édité :++:
(Fais gaffe quand tu mets de "!" juste après un nombre, j'ai cru que c'était une factorielle :ptdr: )

[Combattant204]

Ca y est, j'ai édité :++:
(Fais gaffe quand tu mets de "!" juste après un nombre, j'ai cru que c'était une factorielle :ptdr: )

Merci j'ai tout a fait compris ce que vous avez explique, mais comment resoudre
2^n = 4.6561
Ou encore(1/2)^n = 1/(4.6561)
Lorsque l'inconnu est en exposant?
:hein:

[capitaine nuggets]

Merci j'ai tout a fait compris ce que vous avez explique, mais comment resoudre
2^n = 4.6561
Ou encore(1/2)^n = 1/(4.6561)
Lorsque l'inconnu est en exposant?
:hein:

Avant tout ce qu'il faut savoir, c'est qu'il s'agit d'exo pour 1re S, donc ils ont été fabriqués de telle manière que les calculs s'arrangent et soient assez réalisables.

De toute manière, quelle que soit la formule de que j'ai donné, le nombre de termes sera le même (heureusement ^^).
Pour résoudre (ou encore , ces équations sont équivalentes).

Il faut y aller à la main :
En divisant par , équivaut à .
Divise membre à membre par et ce, jusqu'à obtenir une puissance de connue.
Après avoir fait ces divisions successives tu tomberas peut-être sur l'égalité : .
Là, tu te dit que , donc d'où .

[Combattant204]

Avant tout ce qu'il faut savoir, c'est qu'il s'agit d'exo pour 1re S, donc ils ont été fabriqués de telle manière que les calculs s'arrangent et soient assez réalisables.

De toute manière, quelle que soit la formule de que j'ai donné, le nombre de termes sera le même (heureusement ^^).
Pour résoudre (ou encore , ces équations sont équivalentes).

Il faut y aller à la main :
En divisant par , équivaut à .
Divise membre à membre par et ce, jusqu'à obtenir une puissance de connue.
Après avoir fait ces divisions successives tu tomberas peut-être sur l'égalité : .
Là, tu te dit que , donc d'où .

Merci je pense avoir vraiment saisit cette methode apres l'avoir lu 6-8 fois :lol3:

Pouvez vous me guider dans la 3eme question?
Je pense qu'il faut la resoudre comme ca
On decompose S en S1 et S2,les 2 auront pour raison 1/9
S1 (comporte les nombres positifs uniquement) et S2(comporte les nombres negatives uniquement.)
Soit S1 = 1/3 + 1/27 + ... + 1/2187
Et S2 =-1/9 - 1/81 - ... - 1/6561
Et S sera telle que
S = S1 + S2
Est il juste de faire ca ou y'a-t-il autre chose???

[capitaine nuggets]

Merci je pense avoir vraiment saisit cette methode apres l'avoir lu 6-8 fois :lol3:

Pouvez vous me guider dans la 3eme question?
Je pense qu'il faut la resoudre comme ca
On decompose S en S1 et S2,les 2 auront pour raison 1/9
S1 (comporte les nombres positifs uniquement) et S2(comporte les nombres negatives uniquement.)
Soit S1 = 1/3 + 1/27 + ... + 1/2187
Et S2 =-1/9 - 1/81 - ... - 1/6561
Et S sera telle que
S = S1 + S2
Est il juste de faire ca ou y'a-t-il autre chose???

Comme tu as pu le remarquer, les signes "+" et "-" sont alternés suivant la parité du terme en question. C'est parce qu'en fait, est la somme de ??? termes consécutifs d'une suite géométrique de raison strictement négative : .
:+++: