Suite et algorithme

[giiseh]

Bonjour
je suis arrivee a la question 1a et 2a mais les autres questions non

Entrée
Saisir n (n entier, n supérieur ou égal à 1)
Initialisation
u prend la valeur 1
Traitement
pour i allant de 1 jusqu'à n
u prend la valeur 2u +i -1
afficher u
FinPour

1) a)on applique cet algorithme pas à pas : on donne par exemple à n la valeur 6 et on note l'évolution des variables dans un tableau.
Compléter ce tableau:

i ... 1 2 ....
u 1 2 5 ....

b) L'algorithme affiche les termes d'une suite générée par une relation de récurrence.
donner la définition de cette suite et préciser les termes affichés par l'algorithme.

c) Coder cet algorithme a l'aide d'une calculette

4) Modifier l'algorithme de telle façon que seul le terme de rang n soit affiché.

5) Corriger le programme

6) Calculer u17 et u26 à l'aide programme.

Merci de bien vouloir m'aider...

[Shew]

Bonjour
je suis arrivee a la question 1a et 2a mais les autres questions non

Entrée
Saisir n (n entier, n supérieur ou égal à 1)
Initialisation
u prend la valeur 1
Traitement
pour i allant de 1 jusqu'à n
u prend la valeur 2u +i -i
afficher u
FinPour

1) a)on applique cet algorithme pas à pas : on donne par exemple à n la valeur 6 et on note l'évolution des variables dans un tableau.
Compléter ce tableau:

i ... 1 2 ....
u 1 2 5 ....

b) L'algorithme affiche les termes d'une suite générée par une relation de récurrence.
donner la définition de cette suite et préciser les termes affichés par l'algorithme.

c) Coder cet algorithme a l'aide d'une calculette

4) Modifier l'algorithme de telle façon que seul le terme de rang n soit affiché.

5) Corriger le programme

6) Calculer u17 et u26 à l'aide programme.

Merci de bien vouloir m'aider...

u = 1; i = 1

u = 2*1 + 1 - 1 = 2

u = 2; i = 2

u = 2*2 + 2 - 2 = 4

u = 4; i = 3

u = 2*4 + 3 - 3 = 8

etc .... jusqu'a ce que i = n

[giiseh]

ca c'est pour la premiere question je l'ai déjà faite c'est la suite que je n arrive pas

[Shew]

ca c'est pour la premiere question je l'ai déjà faite c'est la suite que je n arrive pas

La suite est recurrente et dans tous les cas on a n - n = 0 (dont je ne comprends pas le but) donc

[giiseh]

c pas Un=2Un+(n+1)-1=2Un+n

[Shew]

c pas Un=2Un+(n+1)-1=2Un+n

C'est bien u = 2u + i - i qui vous avez écrit dans l'enoncé ?

[giiseh]

Ah non je me suis trompé c'est 2u+i-1

[Shew]

Ah non je me suis trompé c'est 2u+i-1

Donc u = 1; i = 1

u = 2*1 + 1 - 1 = 2

u = 2; i = 2

u = 2*2 + 2 - 1 = 5

u = 5; i = 3

u = 2*5 + 3 - 1 = 12


De ce qui précède on a bien :

[mathelot]

bonjour,
il faut bien que tu distingues:
- une suite définie par récurrence
- une suite définie par algorithme

ce qui différe, ce sont les numérotations possibles des termes de la suite
(des valeurs prises) . Quand la valeur initiale vaut 1 par programme,
on peut numéroter, arbitrairement, à partir de l'indice 0 ou de l'indice 1, ou de l'indice 150.

ce qui donnerait
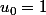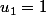ou ou

de plus ton instruction itérative u=u+i-i est fausse.

Le plus simple est d'indicer avec le compteur de boucle , mais ce n'est pas obligé,
le compteur de boucle ne sert qu'à égréner les termes.

[Cliffe]

c'est le nouveau programme les algo à la calculette ?

[mathelot]

oui................

[giiseh]

ok merci j'y suis arrivée apres pour la question 2a j ai dit qu il fallait echanger afficher u et fin pour mais apres je ne vois pas ce qu il faut corriger pour le programme la question b et c

[mathelot]

tu peux corriger cette ligne que j'y vois plus clair ?

u prend la valeur 2u +i -i

[paquito]

L'algorithme demande d'afficher u après chaque nouveau calcul de u, ce qui ne sert à rien puisque l'on ne verra rien sauf si on ajoute une instruction pause pour pouvoir lire , , 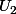etc...,jusqu'à que l'on pourra lire puisque le programme se sera arrété.

Donc au lieu de:

Afficher U
Finpour

Tu fais

Finpour
Afficher U

Sinon pour définir ta suite, n'oublie pas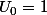


Comme tu a l'air d'être embêté avec la programmation de ta calculatrice, je vais te donner celui sur TI; ça te servira de modèle pour un autre calcul de suite définie par récurrence;

rompt N
:1->U
:For(I,1,N)
:2U+I-1->U
:End
isp U

tu vois que c'est pas méchant!

[giiseh]

Pour la dernière question j'ai trouvé U17=262 126 et U26=134 217 189

[paquito]

ma calculatrice me donne U_26=134 217 701, mais on va dire que c'est bon! j'ai U_17=262 126, donc ça marche!