Bonjour tout le monde,besoin d'aide.
On cherche les entiers a tels que a^2 - 1 soit divisible par 4.
1.A l'aide de la calculatrice ou d'un tableur,emettre une conjecture.
2.Demontrer cette conjecture.
1.je calcule:
Pour a = 1 reste dans la division de a^2 - 1 par 4 est 0
Pour a = 2 reste dans la division de a^2 - 1 par 4 est 3
Pour a = 3 reste dans la division de a^2 - 1 par 4 est 0
Pour a = 4 reste dans la division de a^2 - 1 par 4 est 3
Pour a = 5 reste dans la division de a^2 - 1 par 4 est 0
Pour a = 6 reste dans la division de a^2 - 1 par 4 est 3
Pour a = 7 reste dans la division de a^2 - 1 par 4 est 0
Conjecture: pour a impair a^2 - 1 est divisible par 4.
2. un nombre impair s'ecrit 2k + 1 (k E Z)
Ensuite quoi faire....? Jsuis arriver a la seulement.
Spe maths (Divisibilite)
7 messages
- Page 1 sur 1
Sylviel a écrit:Et bien pose
1) a = 2k+1, calcule a²-1 et déduis en ce que tu veux
2) a = 2k, calcule a²-1 et déduis en ce que tu veux
Merci trop!!!
D'ou a s'ecrit a^2 - 1 = (2K + 1)^2 - 1 = 4k^2 + 2k + 1 - 1 = 4(k^2 + k).
Un nombre pair s'ecrit 2k d'ou a^2 - 1 = 4k^2 - 1.
pardon mais je ne vois pas tres bien en quoi ce que j'ai aboutit montre,pouvez vous expliquer?
si a = 2k+1, alors tu as bien montré que a²-1 = 4*truc, donc que a²-1 est divisible par 4.
si a = 2k pour conclure tout dépend de ce que tu connais. Connais tu les modulos ?
Sinon il faut faire par l'absurde : suppose que a²-1 est divisible par 4 (ie a²-1 = 4n),
alors tu as
4n = 4k^2 - 1
et en jouant un peu avec l'équation tu arrives à une absurdité.
si a = 2k pour conclure tout dépend de ce que tu connais. Connais tu les modulos ?
Sinon il faut faire par l'absurde : suppose que a²-1 est divisible par 4 (ie a²-1 = 4n),
alors tu as
4n = 4k^2 - 1
et en jouant un peu avec l'équation tu arrives à une absurdité.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Sylviel a écrit:si a = 2k+1, alors tu as bien montré que a²-1 = 4*truc, donc que a²-1 est divisible par 4.
si a = 2k pour conclure tout dépend de ce que tu connais. Connais tu les modulos ?
Sinon il faut faire par l'absurde : suppose que a²-1 est divisible par 4 (ie a²-1 = 4n),
alors tu as
4n = 4k^2 - 1
et en jouant un peu avec l'équation tu arrives à une absurdité.
Merci! C claire!
salut
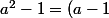(a + 1))
or a - 1 et a + 1 sont deux entiers (consécutifs) de même parité
donc
si a est pair alors a - 1 et a + 1 sont impairs tout comme leur produit ... et ne peut donc être divisible par 4
si a est impair alors a - 1 et a + 1 sont pairs et leur produit est trivialement multiple de 4
:zen:
or a - 1 et a + 1 sont deux entiers (consécutifs) de même parité
donc
si a est pair alors a - 1 et a + 1 sont impairs tout comme leur produit ... et ne peut donc être divisible par 4
si a est impair alors a - 1 et a + 1 sont pairs et leur produit est trivialement multiple de 4
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
