La "sorcière d'Agnesi"
46 messages
- Page 1 sur 3 - 1, 2, 3
La "sorcière d'Agnesi"
salut a tous!!!
jai un autre problème(décidemment c pas mon jour!! :cry: )
Dans le repère orthonormal d'axes (x'x) et (y'y) ,le point fixe P a pour coordonnées (0;2).
Soit C le cercle de diamètre [OP].
La droite d est une droite variable qui pivote autour de P.
Cette droite coupe C en K et x'x) en H.Soit x l'abcsisse de H et y l'ordonnée de K.M est le point de coordonnées (x;y).
La courbe décrite par le point M lorsque d pivote autour du point P a été étudié par Maria Gaetana Agnesi.
On peut la tracer au moyen d'un logiciel.
1)Soit m la pente variable de la droite d.=>c quoi la pente variable??
Montrer qu'une équation de cette droite est y=mx+2.=>comment faire?
Montrer qu'une équation du cercle C est x²+(y-1)²=1.=>fautil utiliser des points de la courbe comme P et K??
2)En déduire les coordonnées des points H et K en fonction de m.
3)Montrer que les coordonnées x et y du point M sont liées par la relation y=(2x²)/(x²+4).comment faire parce que là je sais pas du tout.
4)Intuitivement,en imaginant le mouvement de la droite d et des points variables,que se passe t-il pour y lorsque x tend vers +oo?vers -oo?
Que se passe til pour x lorsque y tend vers 1 par valeurs intermédiares?vers 1 par valeurs supérieures??
il parle de x et y mais il parle des axes??ou de points??si oui lesquels??
5)Retrouver les limites étudiées de manière intuitive dans la question précédente.
sa je saurais le faire
6)Etudier la fonction f définie sur R par f(x)=(2x²)/(x²+4).Tracer la courbe représentative de f(courbe décrite par M).Cest cette courbe que lon nomme "sorcière d'Agnesi".
Est ce que je doit étudier les variations??
merci de maider parce que jy arrive pas du tout!! :marteau: et sa fait 3 heures que je suis dessus si ce nest +!!merci de votre aide!! :cry:
jai un autre problème(décidemment c pas mon jour!! :cry: )
Dans le repère orthonormal d'axes (x'x) et (y'y) ,le point fixe P a pour coordonnées (0;2).
Soit C le cercle de diamètre [OP].
La droite d est une droite variable qui pivote autour de P.
Cette droite coupe C en K et x'x) en H.Soit x l'abcsisse de H et y l'ordonnée de K.M est le point de coordonnées (x;y).
La courbe décrite par le point M lorsque d pivote autour du point P a été étudié par Maria Gaetana Agnesi.
On peut la tracer au moyen d'un logiciel.
1)Soit m la pente variable de la droite d.=>c quoi la pente variable??
Montrer qu'une équation de cette droite est y=mx+2.=>comment faire?
Montrer qu'une équation du cercle C est x²+(y-1)²=1.=>fautil utiliser des points de la courbe comme P et K??
2)En déduire les coordonnées des points H et K en fonction de m.
3)Montrer que les coordonnées x et y du point M sont liées par la relation y=(2x²)/(x²+4).comment faire parce que là je sais pas du tout.
4)Intuitivement,en imaginant le mouvement de la droite d et des points variables,que se passe t-il pour y lorsque x tend vers +oo?vers -oo?
Que se passe til pour x lorsque y tend vers 1 par valeurs intermédiares?vers 1 par valeurs supérieures??
il parle de x et y mais il parle des axes??ou de points??si oui lesquels??
5)Retrouver les limites étudiées de manière intuitive dans la question précédente.
sa je saurais le faire
6)Etudier la fonction f définie sur R par f(x)=(2x²)/(x²+4).Tracer la courbe représentative de f(courbe décrite par M).Cest cette courbe que lon nomme "sorcière d'Agnesi".
Est ce que je doit étudier les variations??
merci de maider parce que jy arrive pas du tout!! :marteau: et sa fait 3 heures que je suis dessus si ce nest +!!merci de votre aide!! :cry:
Bon restons calmes... PAS DE PANIQUE !!!!!!!!!!! (moi non plus d'ailleurs, pas de panique .... :marteau: )
Ben comme la droite d pivote, elle a une pente qui varie.
Bon tu sais déjà que la pente de cette droite est m (on te l'a dit juste avant :id: ), donc y = mx + b.
Et b est l'ordonnée à l'origine de cette droite, c.a.d l'ordonnée du point auquel d coupe l'axe des ordonnées (c'est pas clair, ça, si ?)
Donc ici, on sait que d coupe (y'y) en P, d'ordonnée 2.
D'où b=2, et y = mx + 2
Jusque là, c'est bon ?
c quoi la pente variable??
Ben comme la droite d pivote, elle a une pente qui varie.
Montrer qu'une équation de cette droite est y=mx+2
Bon tu sais déjà que la pente de cette droite est m (on te l'a dit juste avant :id: ), donc y = mx + b.
Et b est l'ordonnée à l'origine de cette droite, c.a.d l'ordonnée du point auquel d coupe l'axe des ordonnées (c'est pas clair, ça, si ?)
Donc ici, on sait que d coupe (y'y) en P, d'ordonnée 2.
D'où b=2, et y = mx + 2
Jusque là, c'est bon ?
Montrer qu'une équation du cercle C est x²+(y-1)²=1
Oui, absolument, il faut utiliser les points, mais pas seulement.
Tu sais que si on note (a,b) les coordonnées du centre d'un cercle et R son rayon, on a que l'équation du cercle est :
(x-a)² + (y-b)² = R²
Ici, le centre du cercle est le milieu de [OP], donc de coordonnées (0,1).
Et le rayon vaut 1, donc :
x² + (y-1)² = 1 est l'équation du cercle C.
(Je ne te conseillerai jamais assez de faire un schéma, avec une droite d (n'importe laquelle qui passe par P) à titre d'exemple).
2) En déduire les coordonnées des points H et K en fonction de m.
- pour H :
Tu sais que H est sur (x'x), donc tu connais son ordonnée.
Pour son abscisse, utilise le fait que H est sur (d).
- pour K:
Tu sais que K appartient au cercle (C) et qu'il est également sur (d).
Je te laisse faire. Mais dis-moi ce que tu trouves (si tu bloques, recopie-moi quand même ton raisonnement, que je sache où ça coince).
H (x,0)
Comme H (d), ses coordonnées vérifient l'équation de la droite (d) :
Y(H) = m*X(H) + 2, donc 0=mx+2, d'où : x=-2/m
Donc H (-2/m,0)
K(x,y)
K(d), donc : Y(K)=m*X(K)+2
et K(C): X(K)²+(Y(K)-1)²=1
Il te reste à résoudre cela ...
Commence par remplacer Y(K) par l'expression de la première ligne dans la seconde....
Comme H (d), ses coordonnées vérifient l'équation de la droite (d) :
Y(H) = m*X(H) + 2, donc 0=mx+2, d'où : x=-2/m
Donc H (-2/m,0)
K(x,y)
K(d), donc : Y(K)=m*X(K)+2
et K(C): X(K)²+(Y(K)-1)²=1
Il te reste à résoudre cela ...
Commence par remplacer Y(K) par l'expression de la première ligne dans la seconde....
46 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

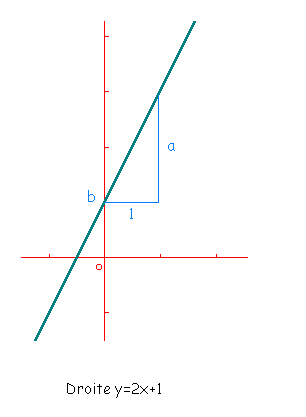
 tient jte met le dessin si sa peut etre plus clair.
tient jte met le dessin si sa peut etre plus clair.