Bonsoir
un exo qui parait simple mais je ne sais comment le traiter
probablement avec des complexes mais.. je sais pas :(
montrer que
cos(pi/13) + cos(3pi/13) + cos(5pi/13) + cos(7pi/13) + cos(9pi/13) + cos(11pi/13) = 1/2
merci bonne soirée ;)
Somme trigonométrique cos((2k+1)pi/13)
8 messages
- Page 1 sur 1
Bonjour,
Je n'ai pas réussi à aller jusqu'au bout mais voici une piste :
Tout d'abord, montre que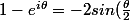e^{i\frac{\theta}{2}}) c'est pas très difficile, multiplie en haut et en bas par
c'est pas très difficile, multiplie en haut et en bas par  ça devrait aller tout seul.
ça devrait aller tout seul.
Ensuite, tu remarques que est la somme des 6 premiers termes d'une suite géométrique de premier terme
est la somme des 6 premiers termes d'une suite géométrique de premier terme 
et de raison donc tu appliques la formule et tu as :
donc tu appliques la formule et tu as :
S=^6)}{1 - e^{2i\frac{\pi}{13}}})
Tu utilises ce que tu as trouvé au début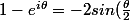e^{i\frac{\theta}{2}}) et tu te retrouves avec :
et tu te retrouves avec :
S=
Enfin, pour avoir ce qu'on veut, tu prends la partie réelle de ce complexe S, ce qui te donne :
=\cos\frac{\pi}{13} + \cos\frac{3\pi}{13} + \cos\frac{5\pi}{13} + \cos\frac{7\pi}{13} + \cos\frac{9\pi}{13} + \cos\frac{11\pi}{13} = \frac{\sin\frac{6\pi}{13}\cos{\frac{6\pi}{13}}}{sin\frac{\pi}{13}})
Voilà... après je vois plus trop quoi faire :p tu dois pouvoir t'arranger avec les fomules d'addition etc, en tout cas quand on le tape à la caltos ça fait bien 1/2 tu peux essayer :p
Bon courage !
Je n'ai pas réussi à aller jusqu'au bout mais voici une piste :
Tout d'abord, montre que
Ensuite, tu remarques que
et de raison
S=
Tu utilises ce que tu as trouvé au début
S=
Enfin, pour avoir ce qu'on veut, tu prends la partie réelle de ce complexe S, ce qui te donne :
Voilà... après je vois plus trop quoi faire :p tu dois pouvoir t'arranger avec les fomules d'addition etc, en tout cas quand on le tape à la caltos ça fait bien 1/2 tu peux essayer :p
Bon courage !
Salut.
Bien sûr qu'en développant en exponentielles on a 12 des 13 racines treizièmes de l'unité, et que comme on sait que la somme des 13 racines est nulle on peut en déduire que comme il manque -1, la somme des exponentielles vaut 1. D'où le résultat cherché qui tombe facilement.
(les 12 racines sont conjuguées deux à deux)
Le problème, c'est que l'on est dans la partie lycée du forum. En l'occurrence, on ne sait pas ça justement. Donc à faire sans racines de l'unité.
@+
Bien sûr qu'en développant en exponentielles on a 12 des 13 racines treizièmes de l'unité, et que comme on sait que la somme des 13 racines est nulle on peut en déduire que comme il manque -1, la somme des exponentielles vaut 1. D'où le résultat cherché qui tombe facilement.
(les 12 racines sont conjuguées deux à deux)
Le problème, c'est que l'on est dans la partie lycée du forum. En l'occurrence, on ne sait pas ça justement. Donc à faire sans racines de l'unité.
@+
c'est effectivement à cela que je pensais : la somme des 12 racines complexes fait 1 et comme on en prend que la moitié, en laissant leurs symétriques, cela fait 1/2. En plus, cette regle se generalise à toutes les racines impaires de -1. exemple : la somme des parties reelles des 5000 premieres racines 10001 eme de -1 fait 1/2...
Il est quand même extraordinaire que l'on apprenne au lycée la notation des complexes sans apprendre aux lycéens les consequences immédiates que cela entraine...
Il est quand même extraordinaire que l'on apprenne au lycée la notation des complexes sans apprendre aux lycéens les consequences immédiates que cela entraine...
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
