Solution d'une équation différentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 24 Déc 2013, 21:17
par Dante0 » 24 Déc 2013, 21:17
Bonjour,
Soit l'équation différentielle :
s -(1-a)(\gamma +n +\delta)v)
On me dit que la solution est

comment l'a -t-on trouvée ?
Ensuite on écrit que la solution générale est
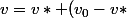e^{-(1-a)(\gamma +n +\delta)t})
complètement perdu.. :hein:
Merci !
Edit : je crois m'être trompé, ce topic aurait peut etre plus sa place en section supérieure... si un modérateur passe par la..


-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 24 Déc 2013, 22:21
par WillyCagnes » 24 Déc 2013, 22:21
bonsoir
1) tu fais v'=0 une Cte
d'où solution particulière
s = (1-a)(\gamma +n +\delta)v*)
v*)
et
)
2)la solution generale, on part de
(\gamma +n +\delta)dt)
(\gamma +n +\delta)t)
d'ou
(\gamma +n +\delta)t))
et k une Cte
en ensuite tu additionnes les 2 solutions
(\gamma +n +\delta)t)+V*)
pour t=0 on a V0
tu obtiens

soit
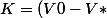)
d'où le resultat cherché
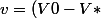.exp(-(1-a)(\gamma +n +\delta)t)+V*)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 24 Déc 2013, 22:53
par Dante0 » 24 Déc 2013, 22:53
WillyCagnes a écrit:bonsoir
la solution generale, on part de
(\gamma +n +\delta)v)
(\gamma +n +\delta)dt)
(\gamma +n +\delta)t)
d'ou
(\gamma +n +\delta)t))
et k une Cte
en ensuite tu derives V et k pour trouver la solution particulière
du genre dk=(1-a)s dt
te laisse faire la suite...
Je ne comprends pas ce que tu fais entre la 1ere et la 2e étape déja, ou est passé le s ?

-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 25 Déc 2013, 09:15
par WillyCagnes » 25 Déc 2013, 09:15
bjr,
voir ma correction ci-dessus
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 25 Déc 2013, 13:06
par Dante0 » 25 Déc 2013, 13:06
Pourquoi poser v'=0 pour la solution particulière ? Sinon c'est compris.
Par contre pour la solution générale, à partir de quelle expression tu calcules la dérivée de v par rapport à v ? (autant dire que les étapes suivantes ne sont pas comprises non plus :(
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 25 Déc 2013, 22:56
par Dante0 » 25 Déc 2013, 22:56
:help::help::help:
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 26 Déc 2013, 19:39
par Dante0 » 26 Déc 2013, 19:39
:help::help::help:
-
Tiruxa
- Membre Relatif
- Messages: 460
- Enregistré le: 22 Oct 2013, 09:21
-
 par Tiruxa » 27 Déc 2013, 11:17
par Tiruxa » 27 Déc 2013, 11:17
Bonjour,
Votre équation est du type y' = ay + b, où a et b sont des réels a étant non nul.
La solution générale de cette équation est l'ensemble des fonctions f définies sur R par :
=K e^{ax}-\frac{b}{a})
où K est une constante réelle.
Voir cours de terminale S pour la démo
la constante K est calculée en prenant x égal à 0
-
Tiruxa
- Membre Relatif
- Messages: 460
- Enregistré le: 22 Oct 2013, 09:21
-
 par Tiruxa » 27 Déc 2013, 11:22
par Tiruxa » 27 Déc 2013, 11:22
Dante0 a écrit:Pourquoi poser v'=0 pour la solution particulière ?
Parce qu'on cherche une solution particulière qui soit une constante donc sa dérivée est nulle.
D'autre part, on cherche ensuite la solution générale de l'équation y' - ay = 0 (dite équation homogène, on annule le second membre qui est au départ égal à b) ce qui fait que le s a "disparu"...
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 27 Déc 2013, 22:17
par Dante0 » 27 Déc 2013, 22:17
-
Tiruxa
- Membre Relatif
- Messages: 460
- Enregistré le: 22 Oct 2013, 09:21
-
 par Tiruxa » 28 Déc 2013, 00:17
par Tiruxa » 28 Déc 2013, 00:17
C'est lorsque l'on résout l'équation homogène c'est à dire y' = ay
On a

Or
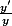
est la dérivée de ln y
d'on en intégrant les deux membres de l'équation on a ln y = ax + C (si la variable est x ou at si c'est t)
Ensuite on utilise l'exponentielle et on obtient y =

en posant K =
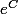
Pour obtenir la solution générale de l'équation de départ il suffit d'ajouter la solution particulière qui est :
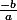
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
?