Sinus et cosinus de π/12
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
PhilipeHook
- Membre Naturel
- Messages: 47
- Enregistré le: 14 Déc 2018, 18:08
-
 par PhilipeHook » 14 Déc 2018, 18:36
par PhilipeHook » 14 Déc 2018, 18:36
Bonjour,
Je galère actuellement sur un exercice de 1èreS (à vrai dire je ne sait pas trop comment le faire).
Dans un carré ABCD de côté a, on trace le triangle équilatéral DMC.
I et J sont les milieux respectifs de [DC] et [AB].(image de la figure) 1) Montrer que MÂJ a pour mesure π/12
1) Montrer que MÂJ a pour mesure π/12
2) Calculer IM, MJ puis AM en fonction du côté a.
3) En déduire les valeurs exactes de cos(π/12) et de sin(π/12)J'ai déjà tenté quelques recherches graphiques (visible sur la photo) même si je doute que cela me mène quelque part.
Merci d'avance pour votre aide.
-
mathelot
 par mathelot » 14 Déc 2018, 19:05
par mathelot » 14 Déc 2018, 19:05
bonjour,
on peut calculer
toutes les mesures d'angles de la figure (en radians) en utilisant successivement les méthodes suivantes:
- la somme des angles d'un triangle vaut

radians
- les angles d'un triangle équilatéral valent
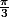
radians
- les angles de base d'un triangle isocèle ont même mesure
les mesures de longueur des côtés se calculent avec le théorème de Pythagore
-
PhilipeHook
- Membre Naturel
- Messages: 47
- Enregistré le: 14 Déc 2018, 18:08
-
 par PhilipeHook » 14 Déc 2018, 19:19
par PhilipeHook » 14 Déc 2018, 19:19
Merci de ta réponse, je savais déjà ce que tu as énoncé dans tes deux premiers tirets.
Mais je n'ais pas saisis pas ce que tu voulais dire dans le troisième.
(Au passage je ne suis donc pas plus avancé)
-
mathelot
 par mathelot » 14 Déc 2018, 19:28
par mathelot » 14 Déc 2018, 19:28
PhilipeHook a écrit:Merci de ta réponse, je savais déjà ce que tu as énoncé dans tes deux premiers tirets.
Mais je n'ais pas saisis pas ce que tu voulais dire dans le troisième.
(Au passage je ne suis donc pas plus avancé)
Quel est la nature du triangle ADM ?
-
PhilipeHook
- Membre Naturel
- Messages: 47
- Enregistré le: 14 Déc 2018, 18:08
-
 par PhilipeHook » 14 Déc 2018, 19:40
par PhilipeHook » 14 Déc 2018, 19:40
Isocèle je suppose, mais si c'est le cas, comment le prouver ?
-
mathelot
 par mathelot » 14 Déc 2018, 19:41
par mathelot » 14 Déc 2018, 19:41
PhilipeHook a écrit:Isocèle je suppose, mais si c'est le cas, comment le prouver ?
cherche un peu, c'est moins difficile que ce que l'on peut en penser.
Modifié en dernier par mathelot le 14 Déc 2018, 20:01, modifié 1 fois.
-
PhilipeHook
- Membre Naturel
- Messages: 47
- Enregistré le: 14 Déc 2018, 18:08
-
 par PhilipeHook » 14 Déc 2018, 20:01
par PhilipeHook » 14 Déc 2018, 20:01
Chose que j'ai faite...
Mais j'en suis parvenu pour la réponse 1 que :
Étant donné que le triangle ADM est isocèle accompagné bien sûr d'une démonstration (que je n'ai pas encore trouvé)
On peut en déduire que :
(AJ ; AM) = (AB ; AD) - (AM ; AD)
= π/2 - 5π/12
= π/12
Dois-je mettre modulo (2π) ?
-
mathelot
 par mathelot » 14 Déc 2018, 20:02
par mathelot » 14 Déc 2018, 20:02
PhilipeHook a écrit:Chose que j'ai faite...
Mais j'en suis parvenu pour la réponse 1 que :
Étant donné que le triangle ADM est isocèle accompagné bien sûr d'une démonstration (que je n'ai pas encore trouvé)
On peut en déduire que :
(AJ ; AM) = (AB ; AD) - (AM ; AD)
= π/2 - 5π/12
= π/12
Dois-je mettre modulo (2π) ?
non, ce n'est pas la peine.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Déc 2018, 07:53
par Carpate » 15 Déc 2018, 07:53
Bonjour,
C'est assez curieux tu exploites très bien le fait que le triangle ADM est isocèle en D mais il ne te saute pas aux yeux que le triangle MCD étant équilatéral et dont le côté CD est commun avec un côté de longueur a du carré ABCD, AD = DM = a
-
PhilipeHook
- Membre Naturel
- Messages: 47
- Enregistré le: 14 Déc 2018, 18:08
-
 par PhilipeHook » 15 Déc 2018, 12:58
par PhilipeHook » 15 Déc 2018, 12:58
Bonjour,
En effet je n'ai pas tilter sur quelque chose pourtant me paraissant maintenant simple.
J'ai donc actuellement ceci pour la question 1) :
Le triangle DMC étant équilatéral et dont le côté DC est commun avec un côté de longueur a du carré ABCD alors AD = DM = a
Ce qui fait du triangle ADM un triangle isocèle.
Étant donné que le triangle ADM est isocèle en D
On peut en déduire que :
(AJ ; AM) = (AB ; AD) - (AM ; AD)
= π/2 - 5π/12
= π/12
Normalement tout est bon.
Mais c'est pour la question deux que ça se gâte.
Je serais tenter de faire un peu comme la partie en déduire (celle un peu plus haut) mais j'ai essayé et ça ne me mène nulle part. Ou bien un peu de théorème de Pythagore mais ne connaissant pas la valeur des côtés...
Et en ce qui concerne la question trois je pense qu'il faut peut être prendre les coordonnées et s'aider de ce qui à été obtenu dans la réponse deux.
-
mathelot
 par mathelot » 15 Déc 2018, 14:27
par mathelot » 15 Déc 2018, 14:27
il s'agit de suivre l'énoncé:
on calcule d'abord IM avec Pythagore ((IM) médiatrice de [C;D]) puis MJ puis AM, toujours grâce à Pythagore
-
PhilipeHook
- Membre Naturel
- Messages: 47
- Enregistré le: 14 Déc 2018, 18:08
-
 par PhilipeHook » 15 Déc 2018, 16:27
par PhilipeHook » 15 Déc 2018, 16:27
Donc si j'ai bien compris j'ai ID = 0.5 ; DM = 1 car a = 1
Ce qui me permet de faire :
sin(M) = opposé/hypoténuse
sin(30)= 0.5/1 ? Ou alors j'ai mal compris.
-
mathelot
 par mathelot » 15 Déc 2018, 16:43
par mathelot » 15 Déc 2018, 16:43
avec Pythagore

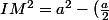^2=\frac{3}{4} a^2)
-
PhilipeHook
- Membre Naturel
- Messages: 47
- Enregistré le: 14 Déc 2018, 18:08
-
 par PhilipeHook » 15 Déc 2018, 18:07
par PhilipeHook » 15 Déc 2018, 18:07
Mais du coup au final en enlevant le carré on obtient moins que 0,75 (a = 1) ce qui est faux (se voit graphiquement).
-
PhilipeHook
- Membre Naturel
- Messages: 47
- Enregistré le: 14 Déc 2018, 18:08
-
 par PhilipeHook » 15 Déc 2018, 18:14
par PhilipeHook » 15 Déc 2018, 18:14
Autant pour moi, petite erreur de calcul (mal écris dans la calculatrice ça donne donc environ 0,86.
-
mathelot
 par mathelot » 15 Déc 2018, 18:29
par mathelot » 15 Déc 2018, 18:29
il faut travailler avec des fractions et des racines carrées, les valeurs décimales approchées ne conviennent pas
pour obtenir les valeurs exactes des sinus et cosinus. Ensuite, la fin de l'exercice est "corsée" et l'on s'en tire en utilisant les valeurs exactes.Avec des valeur décimales, on passe à côté de la démonstration.
Que vaut IM ?
-
PhilipeHook
- Membre Naturel
- Messages: 47
- Enregistré le: 14 Déc 2018, 18:08
-
 par PhilipeHook » 15 Déc 2018, 18:51
par PhilipeHook » 15 Déc 2018, 18:51
IM = Racine carrée de 3/4a
Désolé mais je ne suis pas très familier avec l'éditeur d'équation.
Et en effet ça se corse à la fin, je n'ai absolument aucune idée de comment faire (c'est de que l'on voit actuellement en cours)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Déc 2018, 18:57
par Carpate » 15 Déc 2018, 18:57
IM = Racine carrée de 3/4a

ne fait pas

-
PhilipeHook
- Membre Naturel
- Messages: 47
- Enregistré le: 14 Déc 2018, 18:08
-
 par PhilipeHook » 15 Déc 2018, 19:03
par PhilipeHook » 15 Déc 2018, 19:03
mathelot a écrit:avec Pythagore

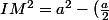^2=\frac{3}{4} a^2)
C'est ce résultat sous racine carrée que je voulais marqué.
-
mathelot
 par mathelot » 15 Déc 2018, 19:05
par mathelot » 15 Déc 2018, 19:05
revois ton calcul de IM:
\frac{\sqrt{3}}{2}a entouré de balise [ tex]et /tex avec des crochets..

Modifié en dernier par mathelot le 15 Déc 2018, 19:12, modifié 1 fois.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités

