Bonjour,
Est ce que f(x) = |x-pi|sin(x) est dérivable sur R ? et comment le démontrer?
F(x) = |x-pi|sin(x) est dérivable sur R
8 messages
- Page 1 sur 1
Re: f(x) = |x-pi|sin(x) est dérivable sur R
Que dire de la dérivabilité de f sur l'ensemble ouvert  ?
?
Re: f(x) = |x-pi|sin(x) est dérivable sur R
La fonction f sur l'ensemble ouvert  est dérivable comme produit de deux fonctions dérivables, en effet, sur cet ensemble, on peut supprimer la valeur absolue.
est dérivable comme produit de deux fonctions dérivables, en effet, sur cet ensemble, on peut supprimer la valeur absolue.
si et si
et si 
si
Re: f(x) = |x-pi|sin(x) est dérivable sur R
julien0683 a écrit:Fonction continue donc dérivable ?
non, il existe des fonctions continues sur R et nulle part dérivables.
Re: f(x) = |x-pi|sin(x) est dérivable sur R
On définit le nombre dérivé de f à droite
=\lim_{ h \rightarrow 0, h>0} \, \dfrac{f(x+h)-f(x)}{h})
le nombre dérivé de f à gauche
=\lim_{ h \rightarrow 0, h<0} \, \dfrac{f(x+h)-f(x)}{h})
f est dérivable en x si et seulement si) et
et ) existent et sont égaux.
existent et sont égaux.
théorème:
soit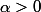
si f est continue sur , dérivable sur
, dérivable sur  et si
et si =l) alors le nombre dérivé à gauche de f en x existe et
alors le nombre dérivé à gauche de f en x existe et =l)
le nombre dérivé de f à gauche
f est dérivable en x si et seulement si
théorème:
soit
si f est continue sur
Re: f(x) = |x-pi|sin(x) est dérivable sur R
calcule f'(x) sur l'intervalle  et sur l'intervalle
et sur l'intervalle 
pour mémoire, une fonction f continue et nulle part dérivable:
=\sum_{k=0}^{+\infty} \, (\dfrac{2}{3})^k \, \sin((\dfrac{5}{2})^k \, x))
pour mémoire, une fonction f continue et nulle part dérivable:
Re: f(x) = |x-pi|sin(x) est dérivable sur R
bonsoir,
le seul problème de dérivation est en
à droite de :
:
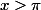
=(x-\pi)sin x)
=sin x +(x-\pi) cos x)
=0)
à gauche de :
:

=(-x+\pi)sin x)
=-sin x +(-x+\pi) cos x)
=0)
f est continue en comme produit de deux fonctions continues.
comme produit de deux fonctions continues.
f est donc dérivable en et
et =0)
le seul problème de dérivation est en
à droite de
à gauche de
f est continue en
f est donc dérivable en
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 179 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
