Signe d'une différence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 07 Nov 2017, 23:27
par yann06 » 07 Nov 2017, 23:27
Bonsoir
 = \left(x-\frac{3}{2}\right)^{2}-\frac{3}{2})
Soient a et b deux réels de [-2 ; 1,5] tel que a < b
Factoriser f(a) - f(b) et étudier le signe de l'expression obtenue
En déduire le sens de variation de la fonction f sur [-2;1,5]
 -f(b) = \left[\left(a - \frac{3}{2} \right)^{2}-\frac{25}{4} \right]-\left[\left(b - \frac{3}{2} \right)^{2} -\frac{25}{4}\right])
 -f(b) = \left(a - \frac{3}{2} \right)^{2}-\frac{25}{4} -\left(b - \frac{3}{2} \right)^{2} +\frac{25}{4})
 -f(b) = \left(a - \frac{3}{2} \right)^{2}-\left(b - \frac{3}{2} \right)^{2})
il ne me reste plus qu'une expression de la forme :

^{2}-\left(b - \frac{3}{2} \right)^{2} = \left(\left(a - \frac{3}{2} \right)+ \left(b - \frac{3}{2} \right) \right)\left(\left(a - \frac{3}{2} \right) - \left(b - \frac{3}{2} \right)\right))
je simplifie ce qu'il y a entre crochets
^{2}-\left(b - \frac{3}{2} \right)^{2} = \left(a + b - \frac{3}{2} - \frac{3}{2} \right) \right)\left(a - b -\frac{3}{2} + \frac{3}{2} \right))
Pour étudier le signe de l'expression obtenue , dois je faire un tableau de signes ??
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 07 Nov 2017, 23:34
par infernaleur » 07 Nov 2017, 23:34
salut, c'est
=(x-3/2)^2-3/2)
ou
=(x-3/2)^2-25/4)
?
Sinon ce que tu as fait me semble juste mais il te faux simplifier la dernière expression que tu as obtenue.
Ce que l'exercice te demande est trouver les variations de la fonction f sur un intervalle en revenant à la définition d'une fonction croissante et d'une fonction décroissante.
C'est à dire si
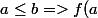 \leq f(b))
(la fonction croissante) ou
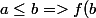 \leq f(a))
(la fonction décroissante)
Toi tu as calculé f(a)-f(b) et l'énoncé suppose que a<b donc une fois que tu auras étudié le signe tu pourras en déduire les variations.
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 08 Nov 2017, 00:27
par yann06 » 08 Nov 2017, 00:27
Ok`
les 3/ 2 s'éliminent dans la seconde expression ( second facteur )
soit
)
et dans le premier :
 = (a + b - 3))
il faut trouver (a + b - 3) ( a +b)
maintenant, comme j'ai un produit de 2 facteurs ( il y'a un signe multiplié) alors dois - je faire un tableau de signe

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 08 Nov 2017, 01:45
par Lostounet » 08 Nov 2017, 01:45
Hi
Je suis un peu curieux quand même: qui te donne de tels exercices à faire? (Ce n'est pas la première fois que je te vois calculer des signes de différences de fonctions de degré 2 de manière...laborieuse!).
À quoi sert-il d' avoir mis f sous forme canonique pour ensuite demander de comparer f(a) et f(b) sachant que... a et b sont du même côté par rapport au sommet de la parabole! Donc on utilise uniquement les variations des fonctions associées !
La fonction carré est croissante sur R+ et décroissante sur R-. Donc (x-3/2)^2 est croissante sur x>=3/2 et décroissante sur x<=3/2.
En ajoutant 3/2 les variations ne sont pas changées. Donc si a<b avec a et b plus petit que 3/2=1.5.. on sait déjà que f(a) > f(b) !
Pas besoin de factoriser quoi que ce soit...c'est contre productif et inutile ici. Et en plus ça semble te bloquer.
Bien sûr tu peux faire le tableau de signes et regarder le signe car tu sais que a-b<0 et aussi que a<=b<=1.5 donc a+b<=3
Ce qui voudrait dire que a+b-3/2-3/2=a+b-6/2=a+b-3 <= 0
Tu as donc un produit de facteurs négatifs...donc le produit est positif et f(a)-f(b)>0 donc f(a)>f(b).. ce qui était évident.
Bref si tu travailles avec un livre.. il faudrait en choisir un autre car celui-ci te donne de mauvais réflexes: pour étudier la croissance d'une fonction, sauf cas très particulier, on ne regarde pas le signe de f(a)-f(b).
Ceci est certes une définition (à savoir) mais elle est pénible à appliquer globalement (à moins de savoir à l'avance sur quel intervalle la fonction est croissante..et cela n'arrive jamais!) Donc il faut préférer d'autres méthodes comme utiliser une combinaison de fonctions de variations connues (ce qui est possible ici via la forme canonique) ou bien plus tard la dérivation.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Black Jack
 par Black Jack » 08 Nov 2017, 10:59
par Black Jack » 08 Nov 2017, 10:59
f(x) = (x - 3/2)² - 3/2
f(a) - f(b) = ((a - 3/2)² - 3/2) - ((b - 3/2)² - 3/2) = (a - 3/2)² - (b - 3/2)² = (a - 3/2 + b - 3/2) * (a - 3/2 - b + 3/2) = (a + b - 3).(a - b)
Comme a < b, (a-b) < 0 et donc f(a) - f(b) a le signe contraire de (a + b - 3)
Avec -2 <= a < b <= 1,5, on a (a + b - 3) < 0 et donc f(a) - f(b) > 0 sur l'intervalle étudié.
Et donc f(x) est décroissante sur [-2 ; 1,5]
*****************
C'est une méthode enseignée lorsque l'élève n'a pas encore appris à dériver et n'est pas encore familier à la manipulation de fonctions élémentaires ... Voire à déterminer le "comportement" de ces fonctions élémentaires avant de pouvoir s'en servir dans l'analyse.

-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 08 Nov 2017, 16:08
par yann06 » 08 Nov 2017, 16:08
Par hypothèse :
je sais que

et que

comme a < b alors a ne sera jamais égal à b
je ne peux pas additionner a et b pour avoir 3
-
Black Jack
 par Black Jack » 08 Nov 2017, 16:58
par Black Jack » 08 Nov 2017, 16:58
yann06 a écrit:Par hypothèse :
je sais que

et que

comme a < b alors a ne sera jamais égal à b
je ne peux pas additionner a et b pour avoir 3
Il est précisé que a < b
On a donc b <= 1,5 ET a < 1,5
--> a + b < 3
a + b - 3 < 0
Qu'est-ce qui te préoccupe avec cela ?

-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 08 Nov 2017, 18:27
par yann06 » 08 Nov 2017, 18:27
Bonsoir
comme on sait que a < 1,5
en fait il ne vaudra jamais 1,5
donc additionnant a et b et bien on n'aura jamais 3
donc on écrit a + b < 3
c'est ça ?
-
Black Jack
 par Black Jack » 08 Nov 2017, 19:10
par Black Jack » 08 Nov 2017, 19:10
yann06 a écrit:Bonsoir
comme on sait que a < 1,5
en fait il ne vaudra jamais 1,5
donc additionnant a et b et bien on n'aura jamais 3
donc on écrit a + b < 3
c'est ça ?
Ben oui.

-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 08 Nov 2017, 19:46
par yann06 » 08 Nov 2017, 19:46
pour trouver le signe de ( a - b)
avec

je vais additionner a et (-b)
à partir de quel hypothèse :

et

ou bien

et

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
