Retrouver une fonction à partir d'un problème

[Sandy1erS]

Bonsoir à tous
Je vous écris en ce jour pour vous demander de l'aide.

voici l'énoncé :
A midi, un bateau A se trouve à 65 km au nord d'un bateau B. Le bateau A se dirige vers le sud a 15km/h pendant que le bateau B fait route vers l'est à 10 km/h.

1/ A 12h+t, A se trouve en A' et B en B'. d(t) = A'B' définie sur R*. Exprimer d(t) en fonction de t, étudier ses variations et trouver à quelle heure les 2 bateaux seront à distance minimale l'un de l'autre.

Voila je n'arrive pas cette première question. j'ai essayé le théorème de pythagore mais je trouve des racines!
Merci de votre aide

[aeon]

C'est quoi ta fonction ?
En quoi c'est un problème d'avoir des racines ?

[Sandy1erS]

Comme on obtient un triangle rectangle A'BB', j'ai fait le théorème de pythagore et je trouve un polynome du second degrès le tout à la racine. Est-ce que c'est juste pour l'instant?

[Huppasacee]

C'est ce qu'on doit obtenir

cependant, on peut dire : lorsque la distance est minimale, le carré de cette distance l'est aussi.

une petite dérivée et vogue la galère !

[Sandy1erS]

donc je peux utiliser le carré de la fonction? je trouve 9 donc la distance minimal est 3. c'est ça?

[Huppasacee]

De toute manière

tu auras
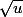
u étant un polynôme du second degré

la dérivée sera , comme tu le sais

donc , étudier les variations de u et celle de sa racine !
le signe de u' décidera pour les 2