Résoudre une équation du 2nd degré "un peu spécial"

par **Coquard** » 04 Oct 2015, 17:19

Bonsoir, je suis en première S,
Je dois résoudre l'équation suivante :

3(x²+x)²-21(x²+x)-180=0

J'ai pensé à développer puis regrouper par terme, enfin utiliser la méthode du discriminant.
Cependant je crois qu'en développant, je me retrouverais avec un x au cube, donc 3rd degré !
Comment la résoudre, en restant sur du 2nd degré ?

par **mathelot** » 04 Oct 2015, 17:22

Pose

ça donne une équation du second degré en Z.

par **Coquard** » 04 Oct 2015, 17:32

Ça donnerais : 3Z²-21Z-180=0
C'est ça ?
Après ça donne : DELTA=b²-4ac --> =(-21)²-4*3*(-180) --> =441+2160 =2601
Puis, x1=12 et x2=-5

C'est bien ça ?

par **titine** » 04 Oct 2015, 18:00

Coquard a écrit:Ça donnerais : 3Z²-21Z-180=0
C'est ça ?
Après ça donne : DELTA=b²-4ac --> =(-21)²-4*3*(-180) --> =441+2160 =2601
Puis, x1=12 et x2=-5

C'est bien ça ?

L'équation. 3Z² - 21Z - 180 = 0 a en effet 2 solutions Z1=12 et Z2=-5
Donc les solutions de 3(x²+x)² - 21(x²+x) - 180 = 0 sont les nombres x qui vérifient x²+x = 12 ou x²+x = -5
Il faut donc maintenant résoudre :
x² + x - 12 = 0
et x² + x + 5 = 0
.........

par **Coquard** » 04 Oct 2015, 18:10

Donc,

Pour x²+x-12=0 : Delta : 49 ; x1 = 4 et x2 = -3

Pour x²+x+5=0 : Delta : -19 donc pas de racines.

Je ne vois pas ce que ça apporte pour la suite puisque si l'on remplace x par 4 ou -3 cela ne donne ni 12 ni -5

par **Coquard** » 04 Oct 2015, 18:31

En fait,

Pour, x²+x-12=0 : x1 = 3 et x2 = -4.

Donc 3²+3=12 : 12 = 12 ; (-4)²+(-4)=12 : 12 = 12.

Donc les solutions de l'équation sont 3 et -4 ?

par **titine** » 04 Oct 2015, 18:33

Coquard a écrit:En fait,

Pour, x²+x-12=0 : x1 = 3 et x2 = -4.

Donc 3²+3=12 : 12 = 12 ; (-4)²+(-4)=12 : 12 = 12.

Donc les solutions de l'équation sont 3 et -4 ?

C'est bien ça.

par **Coquard** » 04 Oct 2015, 19:37

Ok merci, juste je n'ai compris le x²+x=Z mais pourquoi après il ne faut rien changer après ?

par **titine** » 04 Oct 2015, 19:54

Coquard a écrit:Ok merci, juste je n'ai compris le x²+x=Z mais pourquoi après il ne faut rien changer après ?

Je ne comprends pas ce que tu veux dire.
On doit résoudre
3(x²+x)²-21(x²+x)-180=0
On remarque que si on pose Z=x²+x on obtient une équation du second degré en Z : 3Z² - 21Z - 180 = 0
Les solutions de 3(x²+x) - 21(x²+x) - 180 = 0 sont donc les nombres x vérifiant :
(x² + x = Z) et (3Z² - 21Z - 180 = 0)
C'est à dire (x² + x = Z) et (Z=12 ou Z=-5)
C'est à dire (x² + x = 12) ou (x² + x = -5)

par **zygomatique** » 04 Oct 2015, 22:30

salut

il est quand même triste de ne pas connaître ses tables de multiplication et écrire

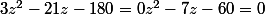
il suffit alors de remarquer que 5 - 12 = -7 et 5 * (-12) = - 60

...

:zen:

Résoudre une équation du 2nd degré "un peu spécial"

Résoudre une équation du 2nd degré "un peu spécial"

Qui est en ligne