Résoudre Xn = Z

par **JC_Master** » 24 Oct 2005, 16:50

Voila, je vien de me poser une question, a partir de

, comment trouver

pour

?

Je trouve

donc

mais sa ne donne pas n ?!

par **Chimerade** » 24 Oct 2005, 17:02

En quelle classe es-tu ?
Que vaut

?

par **JC_Master** » 24 Oct 2005, 17:10

Je suis en début de seconde. Donc si il faut utiliser des outils que je ne conais pas, il faut détailler a font le résonement :marteau:

Sinon

vaut.............. 0! Non je blague, il vaut 1.

par **Chimerade** » 24 Oct 2005, 17:30

JC_Master a écrit:Voila, je vien de me poser une question, a partir de , comment trouver pour ?

Je trouve donc mais sa ne donne pas n ?!

Si

est égal à 1,

est un entier pair à partir de n=1. Il ne peut donc jamais être égal à 35273 qui est assez fortement impair !

par **JC_Master** » 24 Oct 2005, 18:35

A oui, donc dans ce cas, il faut trouver la valeur de n par exée qui se raproche le plus de

:we:

par **LN1** » 24 Oct 2005, 19:26

Bon, tu remarques que

Tu cherches donc le premier entier n tel que

dépasse 35273

Si tu peux travailler à la main, tu peux procéder par tâtonnement 2

(trop petit)
2

trop grand etc...

Si tu veux le faire directement, il faut utiliser un outil que tu ne connais pas qui est la fonction

par **JC_Master** » 24 Oct 2005, 20:56

Ah! Sur le coup j'y avais pas pensser.
Et sinon,

, on peut pas résoudre sa pour noter

Et sinon comment fonction

?

par **LN1** » 24 Oct 2005, 21:17

Bon j'essaie de te donner des infos accessible en seconde. Une définition plus rigoureuse te sera donnée en terminale.

est une fonction qui te permet de trouver l'exposant d'un puissance de 2

quel est alors son effet sur un nombre qui n'est pas une puissance entière de 2 ? et bien cela donne un exposant non entier...

car

Sur ta calculette il est possible que tu ne trouves pas la fonction

Mais tu apprendras que

Si tu calcules

, tu trouves environ 15,10
donc la puissance de 2 immédiatement supérieure à 35273 est 16, donc n = 15

en langage mathématique tu auras

par **JC_Master** » 24 Oct 2005, 21:40

Ok jusque l'a j'ai compri, sauf pour

Sinon, je sais que je suis curieux mais, comment fonctionne

? Ou d'abord comment fonctione

?

par **LN1** » 24 Oct 2005, 22:02

Ceci est une longue histoire qui ne tient pas sur un forum
tu peux déjà lire
http://serge.mehl.free.fr/chrono/Neper.html
ou bien une bonne encyclopédie

Quant à log_2(x) = log(x)/log(2) tu peux l'admettre
ou bien, si tu as compris qu'un logarithme transforme un produit en somme, tu peux comprendre que ça transforme une puissance en produit
log(2*2*2*2...*2) = log(2) + log(2) + ... + log(2)

en généralisant à des exposants non entiers

donc

par **JC_Master** » 24 Oct 2005, 22:40

n remarquera que si une suite (un) de nombres est géométrique de la forme

, a constant,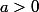

, a 1 (a est la raison de la suite), alors le "logarithme" dans la base a de un est une suite arithmétique (

) de raison 1 : par passage au logarithme, les multiplications deviennent des additions.

Maleureusement je ne comprend pas tout ce qui est en DarkRed :cry:

par **julian** » 25 Oct 2005, 08:26

Bonjour,
Et bien tu as sûrement dû voir les suites arithmétiques dont la définition est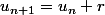

, avec

est la raison de la suite arithmétique

. (enfin çà ne se voit qu'en 1ère théoriquement mais tu as l'air d'en avoir entendu parler).
Et bien dans les suites numériques il y a aussi les suites géomètriques dont la définition est

, avec q la raison de la suite géométrique

.

Et lorsque tu as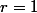

par exemple dans une suite arithmétique, tu dis que la raison de

est 1.
:++:

par **JC_Master** » 30 Oct 2005, 21:12

Maleuresuement non je n'en ai pas entendu parler, enfaite la petite mais bien enbètent équation X_{n+1} = 2X_n vien du calcule des racines carée avec l'algorithme d'alexandrie. D'après ce que l'on ma dit, a chaque itération la présision des décimales doubles, donc pour savoir quèl doit être le nombre d'itération pour un nombre de décimale n, il faut résoudre cette équation.
Et mentenant je vais devoir comprendre comment programmer log pour programer

(

revien bien a Racine

ième ?)

Je ne conais ni les suites aritmétiques, ni les suites numériques, et je ne sais pas ce qu'est une "raison". Mais j'aime vraiment les mathes, alors quand je peut trouver des esplications que j'arive a comprendre, je profite de l'ocasion pour savoir. J'ai toujours une question a poser, mais je ne suis pas toujour capable de comprendre la réponse...

par **LN1** » 30 Oct 2005, 21:22

Si c'est pour programmer une boucle, tu peux faire un test à l'intérieur de ta boucle ou bien une boucle while

while X < nb de décimales
[...
...
X = 2X]

par **JC_Master** » 30 Oct 2005, 21:35

Enfaite c'est pour réécrire les outils mathématique.
On done un nombre de décimale

, on calcule

et on itère

fois.
Mais esque je pourais être éclairer sur "la trensformation en adition" ?

Résoudre Xn = Z

Résoudre Xn = Z

Qui est en ligne