Resoudre equation exp(x)-ln(x)=0

[ghalyb24]

Bonjour,
svp j'ai un probleme dans la resolution de l'equation exp(x)-ln(x)=0.
Merci de m'aider.

[laetidom]

Bonsoir,

Ce qui signifierait que = . . . ?

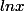Or les 2 courbes représentatives des fonctions sont symétriques par rapport à ?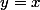



Dans ce cas de figure, peut-on alors avoir une égalité ?

.

[Tiruxa47]

Bonjour,

Oui et surtout la courbe représentant ln est situé strictement au dessous de la droite d'équation y=x.

On peut pour le justifier étudier la fonction f définie sur ]0;+inf[ par f(x)= lnx - x
son maximum est f(1)=-1.

[Lostounet]

Bonjour,
svp j'ai un probleme dans la resolution de l'equation exp(x)-ln(x)=0.
Merci de m'aider.

Il est clair que l'équation n'a pas de solutions (réelles) !
Par contre, que dire de l'exercice suivant (que je viens d'inventer) :

Discuter, selon les valeurs de la constante réelle c, le nombre de solutions de l'équation