Résoudre x^3-1=0 dans R

[craboulleur]

Bonjour, j'ai un petit problème, je n'arrive pas à résoudre cette équation dans R : x^3-1=0 , une solution est évidente : 1 mais comment montrer qu'il n'y en a pas d'autres ou y en a t il d'autres ?

si vous pouviez m'aider ce serait cool

[Mimosa]

Bonjour

Non, il n'y en a pas d'autres. Mets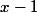 en facteur et étudie le trinôme du second degré qui apparaît.

[hdci]

Bonjour,

Selon ton niveau, su tu as vu ce que sont les dérivées, tu peux également étudir les variations de la fonction et en déduire qu'il n'y a qu'une seule solution (et comme tu l'as trouvée...)

[Carpate]

Identité remarquable :

et en point bonus (b changé en -b) :

[craboulleur]

Merci pour vos réponse, j'ai utilisé la technique de Mimosa qui m'a donné :

x^3-1=(x-1)(ax^2+bx+c)
j'ai développé:
cela donne : x^3-1=ax^3+bx^2+cx-ax^2-bx-c

comme on veut retrouver x^3-1, on doit avoir bx^2-ax^2=0 et cx-bx=0 et comme c=1 vu que l'on a -c, on en déduit que a=1 ; b=1 et c=1, on trouve au final x^3-1=(x-1)(x^2+x+1)=0

d'une part (x-1)=0 et d'autre part (x^2+x+1)=0 comme cela on prouve que l'unique solution est 1, est-ce bon ?

merci pour les identités remarquable Carpate, je ne les connaissaient pas

[hdci]

Oui c'est cela. Il faut néanmoins savoir dire pourquoi 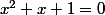n'admet pas de solutions (dans , car il existe d'autres ensembles dans lesquels il y a des solutions)

[craboulleur]

oui on peut faire delta : delta= b^2-4ac = 1^2-4*1*1=-3 , dans R , x^2+x+1 n'admet donc pas de solution

[hdci]

C'est tout bon.

[Black Jack]

Salut,

x³-1 = 0

x = 1 est une solution triviale et donc x³-1 est divisible par (x-1).

Si on ne sait pas faire la division euclidienne alors il suffit alors de faire apparaître ce "facteur" (x-1)

x³ - 1 = x³ - x² + x² - x + x - 1
= x²(x-1) + x(x-1) + (x-1)
= (x-1).(x² + x - 1)

...