[Résolu]Reflexion parabolique

[Ito]

Bonjour,

J'ai l'exercice de math suivant :

Démontrer qu'il existe un point F situé sur l'axe d'une parabole tel que tous les rayons paralleles à cet axe sont focalisés par réflexion en ce point.

la surface de la parabole d'équation y=ax² est parfaitement réfléchissante. Pour montrer l'existence de F et en donner les coordonnées on appliquera donc le principe de la réflexion sur un miroir.

bon pour commencer j'ai déterminé l'équation (y) de la tangeante à un point A (x0, y0) (en passant par les dérivées). Ensuite j'ai déterminé l'équation (g) de la perpendiculaire à ma tangeante qui passe par le point A.

Maintenant il ne me reste plus qu'à trouver l'équation de la droite qui est la droite symetrique au rayon de soleil d'equation y=x0 par rapport à (g).
Je ne sais plus comment on calcul l'équation d'une droite symétrique à un axe.

Quelqu'un peut-il m'aider.
Merci.

[Quidam]

Bonjour,

Tout d'abord, il est inutile de calculer l'équation de la perpendiculaire à la tangente (pas tangeante !) (la normale), car si D et D' passent par un point A, la symétrique de D par rapport à D' est confondue avec la symétrique de D par rapport à la droite D'' passant par A et orthogonale à D'.

La droite tracée par le rayon réfléchi est donc la symétrique de D par rapport à la tangente.

Ensuite, tu peux évaluer l'angle Ox,D par le coefficient directeur de la tangente D (tan(Ox,D)=a si y=ax+b est l'équation de la tangente)
Tu en déduis l'angle D,Oy (facile). Si D1 désigne la symétrique, tu peux calculer D1,Oy=-(D,Oy), puis (Ox,D1) et enfin tan(Ox,D1) qui sera le coefficient directeur de la droite cherchée.

[Ito]

Merci quidam pour ta réponse.
Je pense que mon énoncé n'est pas trés clair, voiciun schéma :


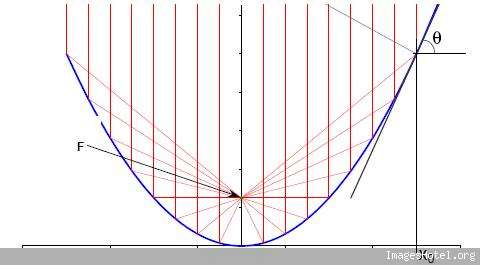
l'équation à la tangente de y=ax² au point (y0;x0) est :
f(x)=(2ax0)*(x-x0)+a(x0)²=2ax0*x -a(x0)²=ax0(2x-x0)
soit B l'angle entre la tangente et la paralèlle à l'axe des ordonnée en (x0) :
Tan B = 2ax0 = pente de la tangente

En utilisant les règle de trigo, on s'apperçois que le rayon réfléchi à pour angle D (soit D l'angle entre le rayon réfléchi et la paralèlle à l'axe des ordonnée en (x0))
D=(2B-Pi/2)

Il ne me reste encore à exprimer tan (2B-Pi/2) en fonction de Tan(B) puis en fonction de X0 et a.

Ensuite j'obtiens un équation de droite et je devrais démontrer que quand x=0, y =1/(4a)

Je n'arrive pas à écrire l'équation du rayon réfléchi de façon simple, même en utilisant un formulaire de trigo.

Quelqu'un peut-il m'aider ? :marteau:

[Huppasacee]

Bonsoir

Soit t la tangente d'un angle a

Les formules de l'angle double donnent
tan 2a = 2t/(1-t²)

La tangente du complémentaire est la cotangente

tan (pi/2 - 2a ) = 1/tan2a = (1-t²)/2t

la tangente de l'angle opposé est l'opposé de la tangente

En résumant

tan(2a-pi/2) = - 1/tan2a = (t²-1)/2t

[Ito]

Merci Huppasacee,

J'avais oublié que :
tan (pi/2 - 2a ) = cotan2a

Donc si je déroule mon exo :

l'équation de mon rayon réfléchi :

y= * x + Cste

Au point (x0, y0) la constante égale :

Cste = y0 - * x0

Donc :

y = * x + y0 - * x0

Si x= 0
y = y0 - * x0

y0 = ax0²

donc y =

CQFD
Merci