Bonjour,
Pour mon grand oral, n'ayant pas d'idée, mon professeur m'a proposer ceci "comment donner une approximation d'un nombre réel à l'aide de suites ?".
J'ai fait plusieurs recherches et exercices mais je ne suis pas du tout certain comment procéder... pouvez-vous m'aider ?
Merci
Serge
Un réel avec une suite - sujet Grand Oral
9 messages
- Page 1 sur 1
Re: un réel avec une suite - sujet Grand Oral
Pour un réel quelconque, on peut l'approcher par une suite de plus en plus précise, en prenant son écriture en base décimale.
Par exemple pour :
:
U0=1
U1=1.4
U2=1.41
...
U8=1.41421356
...
etc infiniment.
Là c'est une suite simple à écrire à la main, mais pas très élégante du point de vue mathématique. C'est néanmoins la suite idéale pour introduire le sujet.
Tu peux parler de dichotomie, pour approcher n'importe quel nombre plus petit que 1
Par exemple pour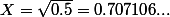
U0=1 : X est plus proche de 1 que de 0, donc on commence avec 1
U1=1-1/2=1/2 : on ajoute ou on retranche 1/2 , pour se rapprocher de X
U2=1/2+1/4 =3/4: on ajoute 1/4, parce que X est plus grand que 1/2
U3=3/4-1/8 : on retranche 1/2, parce que X est plus petit que 3/4
etc
A chaque fois , on fait une division par 2, on a une valeur approchée de plus en plus précise.
Le mot dichotomie vient du grec dikhotomia, qui veut dire "division en 2 parties"
J'ai tapé PI limite de suite sur Google ... je suis arrivé sur cette page https://www.pedagogie.ac-nantes.fr/mathematiques/enseignement/groupe-de-recherche/2017-2019/en-route-vers-pi-1121427.kjsp?RH=1160079471359où on propose 3 suites qui amènent à pi
La suite 1 -1/3+1/5-1/7+1/9-1/11 etc etc tous les nombres impairs, en changeant de signe à chaque fois.
Plus on calcule de termes, plus on se rapproche de Pi.
Des suites construites avec les nombres entiers et qui conduisent vers Pi, il y en a plein,
En 5 minutes, tu ne pourras pas parler de tous ces exemples ... mais tu seras armé pour répondre à des questions ouvertes sur le sujet.
Par exemple pour
U0=1
U1=1.4
U2=1.41
...
U8=1.41421356
...
etc infiniment.
Là c'est une suite simple à écrire à la main, mais pas très élégante du point de vue mathématique. C'est néanmoins la suite idéale pour introduire le sujet.
Tu peux parler de dichotomie, pour approcher n'importe quel nombre plus petit que 1
Par exemple pour
U0=1 : X est plus proche de 1 que de 0, donc on commence avec 1
U1=1-1/2=1/2 : on ajoute ou on retranche 1/2 , pour se rapprocher de X
U2=1/2+1/4 =3/4: on ajoute 1/4, parce que X est plus grand que 1/2
U3=3/4-1/8 : on retranche 1/2, parce que X est plus petit que 3/4
etc
A chaque fois , on fait une division par 2, on a une valeur approchée de plus en plus précise.
Le mot dichotomie vient du grec dikhotomia, qui veut dire "division en 2 parties"
J'ai tapé PI limite de suite sur Google ... je suis arrivé sur cette page https://www.pedagogie.ac-nantes.fr/mathematiques/enseignement/groupe-de-recherche/2017-2019/en-route-vers-pi-1121427.kjsp?RH=1160079471359où on propose 3 suites qui amènent à pi
La suite 1 -1/3+1/5-1/7+1/9-1/11 etc etc tous les nombres impairs, en changeant de signe à chaque fois.
Plus on calcule de termes, plus on se rapproche de Pi.
Des suites construites avec les nombres entiers et qui conduisent vers Pi, il y en a plein,
En 5 minutes, tu ne pourras pas parler de tous ces exemples ... mais tu seras armé pour répondre à des questions ouvertes sur le sujet.
Re: un réel avec une suite - sujet Grand Oral
Correction .. la suite proposée tend vers Pi/4, et pas vers Pi.
Re: un réel avec une suite - sujet Grand Oral
Et pour racine de deux, il y a la méthode d'Héron d'Alexandrie qui est de convergence très rapide
Chercher "suite de Héron" sur Google.
De façon générale, pour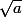 , c'est la suite définie par la relation de récurrence
, c'est la suite définie par la relation de récurrence
)
Et démontrer que cette suite converge vers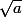 est du niveau terminale (point fixe d'une fonction continue, et sens de variation de la suite).
est du niveau terminale (point fixe d'une fonction continue, et sens de variation de la suite).
Chercher "suite de Héron" sur Google.
De façon générale, pour
Et démontrer que cette suite converge vers
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: un réel avec une suite - sujet Grand Oral
Bonjour
Le nombre d'or est aussi sympa à étudier
Il est limite,en particulier, de la suite) telle que
telle que 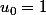 et pour tout entier n ,
et pour tout entier n , 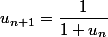 .
.
On peut y retrouver les termes de la suites de Fibonacci (si on écrit les termes sous forme de fractions).
Plus généralement on peut évoquer les fractions continues (voir le début du document suivant)
https://dms.umontreal.ca/~rousseac/chap ... ntinue.pdf
Le nombre d'or est aussi sympa à étudier
Il est limite,en particulier, de la suite
On peut y retrouver les termes de la suites de Fibonacci (si on écrit les termes sous forme de fractions).
Plus généralement on peut évoquer les fractions continues (voir le début du document suivant)
https://dms.umontreal.ca/~rousseac/chap ... ntinue.pdf
Re: un réel avec une suite - sujet Grand Oral
bonsoir,
il y a la suite de Newton-Raphson.
Soit f une fonction dérivable, admettant une racine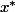 telle que
telle que =0)
de dérivée ne s'annulant pas au voisinage de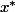
Le but est de calculer des valeurs approchées) de
de 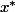 .
.
Après calculs, cette suite vérifie la formule de récurrence:
}{f'(x_n)})
avec proche de
proche de 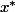
https://fr.wikipedia.org/wiki/M%C3%A9thode_de_Newton
Quand on applique la méthode Newton-Raphson à l'équation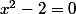 , on retrouve
, on retrouve
la méthode de Héron. Notons que la méthode de Héron du calcul de valeurs approchées
de est illustrée par un raisonnement géométrique: on effectue la moyenne
est illustrée par un raisonnement géométrique: on effectue la moyenne
entre une valeur approchée par excès et une valeur approchée par défaut.Si ces deux valeurs sont
les mesures de longueur des côtés d'un rectangle, à chaque itération ce rectangle devient plus (proche du) carré.
il y a la suite de Newton-Raphson.
Soit f une fonction dérivable, admettant une racine
de dérivée ne s'annulant pas au voisinage de
Le but est de calculer des valeurs approchées
Après calculs, cette suite vérifie la formule de récurrence:
avec
https://fr.wikipedia.org/wiki/M%C3%A9thode_de_Newton
Quand on applique la méthode Newton-Raphson à l'équation
la méthode de Héron. Notons que la méthode de Héron du calcul de valeurs approchées
de
entre une valeur approchée par excès et une valeur approchée par défaut.Si ces deux valeurs sont
les mesures de longueur des côtés d'un rectangle, à chaque itération ce rectangle devient plus (proche du) carré.
Modifié en dernier par mathelot le 22 Juin 2021, 20:42, modifié 5 fois.
Re: un réel avec une suite - sujet Grand Oral
L'exemple que je donnais sur Pi a un côté magique. Par quel miracle cette suite converge-t-elle vers Pi/4.
Aucune idée, et si par hasard un prof te demande de le justifier, ça risque d'être compliqué.
Les 2 exemples sur la méthode d'Heron d'Alexandrie, ou la méthode proposée par Mathelot sont moins piégeux.
Si on te pose des questions, pourquoi ça marche, tu peux avoir des réponses.
Aucune idée, et si par hasard un prof te demande de le justifier, ça risque d'être compliqué.
Les 2 exemples sur la méthode d'Heron d'Alexandrie, ou la méthode proposée par Mathelot sont moins piégeux.
Si on te pose des questions, pourquoi ça marche, tu peux avoir des réponses.
Re: un réel avec une suite - sujet Grand Oral
Comme contre-exemples, il y a des nombres réels (en théorie probabiliste) dont il est impossible (structurellement, ontologiquement impossible) de calculer la moindre décimale, résultat qui m'avait fortement intrigué
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
