Bonjour, je dois démontrer que

est divisible par
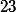
. Ca je pense savoir faire, mais j'ai des doutes pour le démontrer autrement, j'aimerai donc savoir si cela correspond bien, merci d'avance :we: .
Si

alors

, la propriété est vérifiée. Supposons que

est divisible par
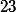
. Montrons qu'alors

est divisible par
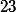
. D'après l'hypothèse de récurrence, il existe un entier naturel q tel que
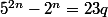
d'où
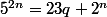
. Par conséquent :
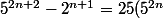-2(2^n)<br />=25(23q+2^n)-2(2^n)<br />=25(23q)+25(2^n)-2(2^n)<br />=25(23q)+2^n(25-2)<br />=23(25q+2^n)<br />=23q')
en posant
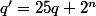
.
donc

est divisible par
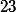
. La propriété est donc vraie pour tout

.
Autre idée :

Pour tout

naturel :

d'où

donc

est divisible par
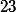
pour tout

naturel.