Radicaux, rationaliser dénominateur, help!, niveau Seconde
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Frencheek
- Membre Naturel
- Messages: 16
- Enregistré le: 15 Sep 2018, 15:34
- Localisation: Washington DC
-
 par Frencheek » 15 Sep 2018, 16:12
par Frencheek » 15 Sep 2018, 16:12
Bonjour !
j'ai fini tous les exercices du chapitre 1 de l'excellent livre "Mise à Niveau Mathématiques" de Josée Hamel, mais j'ai beau la retourner dans tous les sens je bloque sur une expression que je n'arrive pas à rationaliser :
}{\sqrt{a}+3})
merci pour votre aide,
Léa
Modifié en dernier par
Lostounet le 15 Sep 2018, 16:21, modifié 1 fois.
Raison: ajout des balises [Tex]

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 15 Sep 2018, 16:22
par Lostounet » 15 Sep 2018, 16:22
Frencheek a écrit:Bonjour !
j'ai fini tous les exercices du chapitre 1 de l'excellent livre "Mise à Niveau Mathématiques" de Josée Hamel, mais j'ai beau la retourner dans tous les sens je bloque sur une expression que je n'arrive pas à rationaliser :
}{\sqrt{a}+3})
merci pour votre aide,
Léa
Salut Léa,
Ne suffit-il pas de multiplier la fraction par

?
Une autre approche serait de constater que:
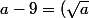^2 - 3^2 =(\sqrt{a}-3)(\sqrt{a}+3))
, ce qui permet immédiatement de simplifier la fraction.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 15 Sep 2018, 16:25
par hdci » 15 Sep 2018, 16:25
Bonjour,
Essayez de poser
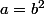
et remplacez

dans votre expression : vous devriez voir apparaître une identité remarquable.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 15 Sep 2018, 16:26
par hdci » 15 Sep 2018, 16:26
Ah, on s'est croisé avec Lostounet

Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
Frencheek
- Membre Naturel
- Messages: 16
- Enregistré le: 15 Sep 2018, 15:34
- Localisation: Washington DC
-
 par Frencheek » 15 Sep 2018, 16:35
par Frencheek » 15 Sep 2018, 16:35
laissez-moi essayer...
-
Frencheek
- Membre Naturel
- Messages: 16
- Enregistré le: 15 Sep 2018, 15:34
- Localisation: Washington DC
-
 par Frencheek » 15 Sep 2018, 16:48
par Frencheek » 15 Sep 2018, 16:48
Merci Hdci et Lostounet, donc en y revenenant :
avant votre réponse j'avais déjà essayé de multiplier la fraction par \frac{\sqrt{a}-3}{\sqrt{a}-3}
mais le livre me donne pour réponse \sqrt{a}-3 alors que moi je me retrouve avec une fraction pleine de racines que je n'arrive pas à simplifier
aussi comme vous suggérez j'ai exploré a=b^{2} et j'ai vu qu'il y avait un lien avec (a+3)(a-3) mais malgré cela je n'arrive pas à "connect the dots" comme on dit en anglais merci d'avance si vous pouvez me donner un second coup de pouce

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 15 Sep 2018, 16:57
par Lostounet » 15 Sep 2018, 16:57
Frencheek a écrit:Bonjour !
j'ai fini tous les exercices du chapitre 1 de l'excellent livre "Mise à Niveau Mathématiques" de Josée Hamel, mais j'ai beau la retourner dans tous les sens je bloque sur une expression que je n'arrive pas à rationaliser :
}{\sqrt{a}+3})
merci pour votre aide,
Léa
Voici la première méthode:
(\sqrt{a}-3)}{(\sqrt{a} + 3)(\sqrt{a} - 3)})
(\sqrt{a}-3)}{(\sqrt{a})^2 - 3^2} = \frac{(a-9)(\sqrt{a}-3)}{a - 9} = \sqrt{a} - 3)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 15 Sep 2018, 17:11
par hdci » 15 Sep 2018, 17:11
... Et pour la seconde méthode :
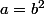
et en prenant

Donc

Maintenant
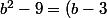(b+3))
(identité remarquable)
D'où
(b+3)}{b+3}=b-3=\sqrt{a}-3)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
Frencheek
- Membre Naturel
- Messages: 16
- Enregistré le: 15 Sep 2018, 15:34
- Localisation: Washington DC
-
 par Frencheek » 15 Sep 2018, 17:27
par Frencheek » 15 Sep 2018, 17:27
pffff trop facile. J'avais fait la bêtise de développer le numérateur et m'étais emmêlé les pinceaux dedans.
Merci Lostounet, c'était plus simple comme ça

Léa
-
Frencheek
- Membre Naturel
- Messages: 16
- Enregistré le: 15 Sep 2018, 15:34
- Localisation: Washington DC
-
 par Frencheek » 15 Sep 2018, 17:28
par Frencheek » 15 Sep 2018, 17:28
hdci a écrit:... Et pour la seconde méthode :
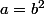
et en prenant

Donc

Maintenant
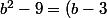(b+3))
(identité remarquable)
D'où
(b+3)}{b+3}=b-3=\sqrt{a}-3)
ça aussi c'est joliment fait. Merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 109 invités
et en prenant
(identité remarquable)