Racine troisième d'un nombre complexe

[novicemaths]

Bonsoir

Je souhaiterais avec une correction, on demande de rechercher la racine troisième d'un nombre complexe.

Pourriez vous me dire si les calculs ci-dessous son juste?

z=-8

Car z = x+yi, ici on a uniquement a.




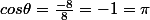
et

Donc



On aura uniquement

K=0



k=1



k=2



Merci.

A bientôt

[Noemi]

Bonsoir novicemaths,

Le début est juste , module et argument de z.
Pour la racine troisième, les arguments sont justes sauf le dernier mais les calculs indiqués ne conduisent pas aux résultats.
Pourquoi cette indication on aura uniquement cos ( ...) ?

[novicemaths]

On a yi=0

[Noemi]

yi = 0 pour le complexe z du départ mais cela ne veut pas dire que pour la racine cubique z est est forcément un réel.
Les arguments trouvés permettent de déterminer la partie réelle et la partie imaginaire du complexe correspondant.

[Carpate]

Une incorrection due à la méconnaissance des priorités : n'a pas de sens mais oui.
Ta rédaction n'est pas claire.
On cherche dans C les racines cubiques de -8, c'est à dire z tel que
Il faut quand même savoir qu'un nombre négatif est un complexe d'argument
D'où les 3 racines, k entier }

[Pisigma]

Bonsoir,







....

[novicemaths]

Je vais refaire les calculs, dois-je donner les résultats sous forme exponentiels?

[mathelot]

Bonsoir

Je souhaiterais avec une correction, on demande de rechercher la racine troisième d'un nombre complexe.

Pourriez vous me dire si les calculs ci-dessous son juste?

z=-8 l'équation est z^3=-8

Car z = x+yi, ici on a uniquement a.




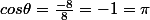
et

Donc ça n'a pas de sens
le cosinus étant compris entre -1 et 1



On aura uniquement

K=0



k=1



k=2



Merci.

A bientôt

[mathelot]

(*)




on pose

Z vérifie l'équation:
on commence par résoudre cette dernière équation.

on note les trois racines cubiques de l'unité solutions de l'équation
:

et

la solution est très employée et a reçu un nom (comme les nombres ou )

les solutions de l'équation (*) sont:
soit

[mathelot]

salut novicemaths,
tu devrais discuter (papoter) pour essayer de comprendre ma réponse et ainsi, progresser en maths.