Quotient de deux logarithmes.

par **mitron** » 07 Jan 2012, 19:31

Bonsoir,

J'aimerais montrer que

= 0 en 0 et en

. (Ce qui est à l'intérieur est une primitive, et on la veut en 0 et en +inf).
En +inf, avec les équivalents on trouve 0. Mais en 0?

Merci.

par **mitron** » 07 Jan 2012, 19:32

0 et +

sont les bornes d'intégration.

par **Ixe** » 07 Jan 2012, 19:51

Salut, peux tu détailler tes calcules ?

par **mitron** » 07 Jan 2012, 19:57

Le calcul de l'intégrale?

Sinon pour le 1/2, ln|1+x| et ln|1-x+x²| ont respectivement pour équivalent en + l'infini, ln|x| et 2ln|x| non?

par **el niala** » 07 Jan 2012, 20:03

juste en passant, l'intégrale de 0 à +

présente un sérieux blème en x=+1 !

pour la limite en +

tu as oublié le "1/3" non ?

pour la limite dans V(0)

~

par **mitron** » 07 Jan 2012, 20:15

Toutes mes excuses, en écrivant en latex, j'ai tendance à m'embrouiller. En réalité, je veux comprendre pourquoi ce terme:

.

En +

c'est OK. La différence des deux ln me donne 0 en utilisant les équivalents.

Mais en 0? faut-il raisonner avec des DL? ln|1+x| ~ x et pour le deuxième terme?

par **el niala** » 07 Jan 2012, 20:39

si c'est

en

un équivalent est

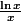
donc limite nulle

en 0, il n'y a aucun souci, le numérateur vaut 0 et le dénominateur 1 !

Quotient de deux logarithmes.

Quotient de deux logarithmes.

Qui est en ligne