Question Fonction Toute Bête
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 04 Oct 2009, 08:32
par Anonyme » 04 Oct 2009, 08:32
Bonjour à vous ,
J'ai une question toute bête à vous poser du niveau 3ème/2nde alors que je suis en 1ère S mais qui ne rentre jamais

!
Il faut trouver l'ensemble de définition de la fonction
)
=
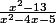
En remarquant que
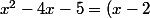^2-9)
, déterminez l'ensemble de définition
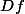
de la fonction

!
Je ne sais jamais si une fonction peut-être négative ou égale à 0 , c'est tout bête , en cours j'y arrive sans réfléchir dans des exercices incluant cette notion mais là ...
J'espère avoir été explicite ! :we:
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 04 Oct 2009, 08:34
par Timothé Lefebvre » 04 Oct 2009, 08:34
Salut :)
Si en fait, elle peut être négative mais pas nulle.
Donc les valeurs interdites, à exclure de R, seront les solutions de (x-2)²-9=0 (qui est un produit de facteurs nul).
Tu comprends ?
PS : comment t'as fait pour mettre ça dans ton pseudo :O le chance ^^
-
Anonyme
 par Anonyme » 04 Oct 2009, 08:43
par Anonyme » 04 Oct 2009, 08:43
Merci , pour cet exemple je fais
^2 = 0)
?
Je comprends pas la fin , je développe
^2-9=0)
! Ou alors je cherche les solutions avec deux facteurs nuls ! Je m'embrouille facilement dans ce genre d'exos désolé !
Ps : Pour les trèfles par exemple , tu fais Alt5

. :we:
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 04 Oct 2009, 08:50
par Timothé Lefebvre » 04 Oct 2009, 08:50
Le produit nul te donne à résoudre (x-2)²-9=0, ce que tu dois factoriser avec une identité remarquable.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 04 Oct 2009, 08:54
par Ericovitchi » 04 Oct 2009, 08:54
il faut que tu suives une logique .
Je récapitule :
- pour que ta fraction soit définie il ne faut pas que le dénominateur s'annule
- le dénominateur c'est
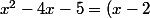^2-9)
donc il faut que je regarde quand est-ce qu'il s'annule
- Pour cela il faut que je trouve les x solutions de l'équation
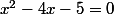
ou encore plus simple que je factorise le polynôme
- comment factoriser ce polynôme. Hé bien en m'apercevant que
^2-9)
est un a²-b²=(a+b)(a-b)
je te laisse finir.
-
Anonyme
 par Anonyme » 04 Oct 2009, 08:56
par Anonyme » 04 Oct 2009, 08:56
Je vais faire :
^2 - (3)^2)
= 0
-3][(x-2)+3])
=0
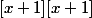
= 0 ?
Désolé je suis lourd
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 04 Oct 2009, 08:57
par Timothé Lefebvre » 04 Oct 2009, 08:57
Euh tu as un petit problème dans ta facto !

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 04 Oct 2009, 08:58
par Ericovitchi » 04 Oct 2009, 08:58
[(x-2)-3][(x-2)+3] =0 ça c'est juste mais après ça déraille
ça fait plutôt (x-5)(x+1) = 0
Bon et donc les deux valeurs de x qu'il faut enlever c'est ?
-
Anonyme
 par Anonyme » 04 Oct 2009, 09:00
par Anonyme » 04 Oct 2009, 09:00
Oui trompé avec la règle du signe - , désolé étourderie !
Donc
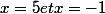
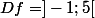
donc
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 04 Oct 2009, 12:03
par Timothé Lefebvre » 04 Oct 2009, 12:03
Re,
non, ton intervalle n'est pas bon. Il faut exclure juste -1 et 5 de R, pas tout ce qu'il y a entre les deux.
On écrira R\{-1;5}.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
