Produit d'entiers consécutifs

[alexis6]

Bonjour,

On démontre assez facilement que le produit de trois entiers consécutifs est toujours divisible par 6. Mais est ce qu'un nombre divisible par 6 est forcément le produit de trois entiers consécutifs? Et comment le démontrer?

[chan79]

Bonjour,

On démontre assez facilement que le produit de trois entiers consécutifs est toujours divisible par 6. Mais est ce qu'un nombre divisible par 6 est forcément le produit de trois entiers consécutifs? Et comment le démontrer?

salut
Essaie avec 12

[alexis6]

salut
Essaie avec 12

OK ca marche pas... Mais alors dans quels cas ca marche?

[Ben314]

Si la question est "Comment repérer si un entier N donné est le produit de 3 nombres consécutifs ?", j'ai bien peur que, une fois vérifié qu'il est multiple de 6 (s'il ne l'est pas, c'est foutu) il n'y ait pas bien de méthode simple...

A la limite, si tu dit que tes 3 entiers consécutifs sont ; et alors le produit des 3 est qui est un peu plus petit que 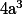(mais pas tellement) donc avec une calculette, tu regarde combien vaut et tu prend pour la partie entière de ce réel là.
Si avec ce là tu n'as pas c'est qu'il ne s'écrit pas comme produit de 3 entiers consécutifs.

[chan79]

OK ca marche pas... Mais alors dans quels cas ca marche?

Pour compléter (si on veut le faire à la main ...)
On a un nombre entier n et on cherche un entier a tel que a(a+1)(a+2)=n.
Tu listes les diviseurs de n.(bon, ça peut être long, comme ci-dessous)
Tu cherches les triplets de diviseurs consécutifs. Tu multiplies pour voir si ça marche.
Exemple: n=24360

1,2,3,4,5,6,7,8,10,12,14,15,20,21,24,28,29,30,35,40,42,56,58,60,70,84,87,105,116,120,
140,145,168,174,203,210,232,280,290,348,406,420,435,580,609,696,812,840,870,1015,1160,
1218,1624,1740,2030,2436,3045,3480,4060,4872,6090,8120,12180,24360
Triplets de diviseurs consécutifs:
1,2,3
2,3,4
3,4,5
4,5,6
5,6,7
6,7,8
28,29,30 c'est le bon !
Si on a algobox sous la main: