Problèmes division et congruence
46 messages
- Page 3 sur 3 - 1, 2, 3
re,
prenons un exemple
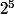 possède 6 diviseurs de la forme
possède 6 diviseurs de la forme  avec
avec 
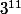 possède 12 diviseurs de la forme
possède 12 diviseurs de la forme  avec
avec 
Les diviseurs du produit sont de la forme:
sont de la forme:
 avec
avec  et
et  variant indépendemment
variant indépendemment
 possède donc
possède donc \times (11+1)=72) diviseurs
diviseurs
pour cette raison, dans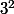 , 3 ne peut pas être d'exposant 2 du fait que n possède 16 diviseurs et que le nombre de diviseurs 16 n'est pas divisible par 3.
, 3 ne peut pas être d'exposant 2 du fait que n possède 16 diviseurs et que le nombre de diviseurs 16 n'est pas divisible par 3.
prenons un exemple
Les diviseurs du produit
pour cette raison, dans
Ca me paraît quand même difficile de traiter cet exercice sans la décomposition en facteurs premiers et le résultat sur le nombre de diviseurs de n. Tentons une explication simple.
Tout d'abord la décomposition en facteur est aussi simple à comprendre qu'elle est délicate à démontrer;
il suffit d'en faire une pour voir que ça marchera: prenons n=60; le plus petit nombre premier est 2; 60 est il divisible par 2? Oui et:
60=2x30; peut on diviser 30 par 2?Oui et
30=2x15; peut on encore diviser 15 par 2, non, passons au nombre premier suivant qui est 3; peut on diviser 15 par 3? oui et
15=3x5; nous sommes arrivés à 5 qui est premier donc 5 est divisible par 5 et:
5=5x1 et nous avons fini puisque par la force des choses:
60=2x2x3x5= 2 a pour valuation 2, 3 a pour valuation 1, 5 a pour valuation 1 et on peut considérer que les autres nombres premier ont pour valuation 0 pour n= 60.
2 a pour valuation 2, 3 a pour valuation 1, 5 a pour valuation 1 et on peut considérer que les autres nombres premier ont pour valuation 0 pour n= 60.
Passons aux diviseurs de 60, tout diviseur de 60 a nécessairement une décomposition de la forme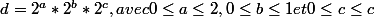 ; comment obtenir tous las cas possibles? En effectuant le produit suivant:
; comment obtenir tous las cas possibles? En effectuant le produit suivant:
(1+2+2^2)(1+3)(1+5); tout les termes de ce produit seront les diviseurs de 60; c'est fait pour et nous aurons 3*2*2=(1+val(2))(1+val(3)(1+val(5))=12; vérifions quand même:
(1+2+4)(1+3)(1+5)=(1+2+4)(1+3+5+15)=1+3+5+15+2+6+10+30+4+12+20+60; on les a bien tous!
Prends des exemples simples pour bien te convaincre.
Revenons a notre exercice: n devant être divisible par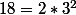 , sa décomposition commencera par
, sa décomposition commencera par avec
avec  ce qui entraîne déjà au moins (1+a)(1+b) diviseurs; si a =2 et b=2, il y aura déjà 9 diviseurs et si on ajoute un nombre premier pour avoir des diviseurs supplémentaires on atteint tout de suite 18 diviseurs, ce qui est trop! donc a=1; si l'on garde a=1 et b=2, il faudrait rajouter 2 facteurs premiers ce qui conduirait à 24 diviseurs, donc prenons b=3 donc déjà 8 diviseurs, mais si on rajoute un facteur premier nous aurons 16 diviseurs; le compte et bon et il est facile de voir que c'est la seule possibilité.
ce qui entraîne déjà au moins (1+a)(1+b) diviseurs; si a =2 et b=2, il y aura déjà 9 diviseurs et si on ajoute un nombre premier pour avoir des diviseurs supplémentaires on atteint tout de suite 18 diviseurs, ce qui est trop! donc a=1; si l'on garde a=1 et b=2, il faudrait rajouter 2 facteurs premiers ce qui conduirait à 24 diviseurs, donc prenons b=3 donc déjà 8 diviseurs, mais si on rajoute un facteur premier nous aurons 16 diviseurs; le compte et bon et il est facile de voir que c'est la seule possibilité.
Conclusion: n=54*p=) avec
avec  et il n'y a que 2 solutions que l'on trouve vite avec un petit programme.
et il n'y a que 2 solutions que l'on trouve vite avec un petit programme.
Tout d'abord la décomposition en facteur est aussi simple à comprendre qu'elle est délicate à démontrer;
il suffit d'en faire une pour voir que ça marchera: prenons n=60; le plus petit nombre premier est 2; 60 est il divisible par 2? Oui et:
60=2x30; peut on diviser 30 par 2?Oui et
30=2x15; peut on encore diviser 15 par 2, non, passons au nombre premier suivant qui est 3; peut on diviser 15 par 3? oui et
15=3x5; nous sommes arrivés à 5 qui est premier donc 5 est divisible par 5 et:
5=5x1 et nous avons fini puisque par la force des choses:
60=2x2x3x5=
Passons aux diviseurs de 60, tout diviseur de 60 a nécessairement une décomposition de la forme
(1+2+2^2)(1+3)(1+5); tout les termes de ce produit seront les diviseurs de 60; c'est fait pour et nous aurons 3*2*2=(1+val(2))(1+val(3)(1+val(5))=12; vérifions quand même:
(1+2+4)(1+3)(1+5)=(1+2+4)(1+3+5+15)=1+3+5+15+2+6+10+30+4+12+20+60; on les a bien tous!
Prends des exemples simples pour bien te convaincre.
Revenons a notre exercice: n devant être divisible par
Conclusion: n=54*p=
46 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
