Un problème

[kabakas]

salut

svp

[LB2]

Bonjour,

que penses-tu de commencer par résoudre ce système pour des petites valeurs de n?

n=1 :
n=2 :
n=3 :

Comment fais tu en général pour passer de n à n+1 ?

[nodgim]

Une autre piste : que vaut ( p + qV3 )* ( p - qV3 ) ?

[Black Jack]

Salut,

Résoudre le système ne présente aucune difficulté.

3 (qn)² = [(2 + V3)^n - V3.qn]² - 1

3 (qn)² = (2 + V3)^2n + 3.(qn)² - 2V3.(2 + V3)^n.qn - 1

(2 + V3)^2n - 2V3.(2 + V3)^n.qn - 1 = 0

qn = [(2 + V3)^2n - 1]/[2V3.(2 + V3)^n]

pn = (2+V3)^n - V3 * [(2 + V3)^(2n) - 1]/[2.V3.(2 + V3)^n]

... pn = pn = [(2 + V3)^(2n) + 1)]/[2.(2 + V3)^n]

Les solutions du système sont :

pn = [(2 + V3)^(2n) + 1)]/[2.(2 + V3)^n]
qn = [(2 + V3)^(2n) - 1]/[2.V3.(2 + V3)^n]

Il reste à montrer qu'elles sont bien dans R²

[aviateur]

Il reste à montrer qu'elles sont bien dans R²

Bonjour
Je pense plutôt qu'il faut montrer que c'est dans


Soit


Donc on pose (donc )
et (donc )
et on a

De plus cela conduit à

[Lostounet]

Salut,
Voici une méthode parmi d'autres:

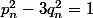
Tout d'abord, il est facile de voir que: d'après l'équation 1, donc:
donc:

Alors: en ayant rendu rationnel le dénominateur.

Nous avons donc:



Par somme et par différence, nous déduisons p_n et q_n.


Maintenant considérons les deux suites et définies comme suit:


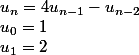
On voit facilement que est toujours un entier naturel (car le terme u_n est obtenu uniquement en multipliant par 4 et soustrayant une valeur plus petite)


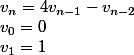
De même v_n est toujours un entier naturel.

Il suffit maintenant de vérifier que p_n et q_n vérifient la même relation de récurrence que u_n et v_n (respectivement) pour conclure que c'est des entiers aussi ! C'est à dire que pn=un et qn=vn pour tout n avec pn et qn les formules explicites des suites (un) et (vn).

[aviateur]

Rebonjour
@ lostounet On peut expliquer d'où vient ta récurrence
En fait on a une première relation de récurrence suggérée par LB2 qui est :
dc

(pour l'obtenir il suffit d'écrire et puis développer)

Si cette relation s'écrit
où
Le polynôme caractéristique de A est : p(x)= x^2- 4x+ 1
d'où et idem pour

[Black Jack]

"Je pense plutôt qu'il faut montrer que c'est dans N²"

C'est ce que j'avais pensé écrire.

[aviateur]

Je m'en doute bien mais c'est normal de rectifier pour le posteur.
Maintenant il ne se manifeste pas alors qu'on rectifie ou pas c'est pareil.

[nodgim]

Je note qu'il n'est pas demandé de donner l'expression de p et q, seulement de prouver que ce sont des entiers.

[LB2]

Je pense que dans cet exercice de niveau terminale S, il est attendu de montrer par récurrence sur n que quelque soit n, il existe des entiers p_n et q_n qui vérifie cette égalité.

Je pense que l'unicité et le calcul de l'expression de p_n et q_n n'est absolument pas attendu au niveau TS.

Cordialement

[nodgim]

Oui, la récurrence, mais pas que.....

[aviateur]

Oui, LB2 tu as raison c'est toi qui à mon avis tu donne la bonne piste pour résoudre le problème au niveau lycée.
Mais perso je donne une solution différente en pensant que la formule du binôme est du niveau du lycée (mais peut être que ce n'est pas le cas?).
Maintenant le posteur ne se manifeste pas et le sujet semble intéresser un peut tout le monde. Donc l'approche de @lostounet est intéressante aussi et si on continue maintenant à en discuter c'est plus pour tout le monde que pour celui qui a posé la question.
Du moins c'est mon point de vue.

[Ben314]

Salut,
Je suis aussi d'accord que, au niveau terminale, la bonne aproche (et de loin), c'est celle de LB2 dans son premier post., c'est à dire de regarder de proche en proche comment s'écrivent les puissance de 2+racine(3).
Après, si effectivement le thread dérive vers "quelle sont tout les point de vue possible sur la question", à mon avis on a quasiment fait le tour en parlant de :
- La conjugaison (i.e. d'introduire (2-racine(3))^n)
- Les suite récurrentes (simple ou double) et le point de vue matriciel de la question.
Et le "quasiment" tient au fait qu'un dernier point de vue (pas vraiment différent mais avec du vocabulaire différent), c'est celui des fractions continues :
2+racine(3) = [3 ; 1 ; 2 ; 1 ; 2 ; 1 ; 2 . . .]
et les P_n et Q_n qui interviennent dans l'énoncé sont des réduites du développement.