Probleme en general
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 24 Oct 2006, 17:26
par bastien83 » 24 Oct 2006, 17:26
le point A a donc pour coordonnée (-1/2;0)???
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 24 Oct 2006, 17:30
par Zebulon » 24 Oct 2006, 17:30
Oui! :happy2:
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 24 Oct 2006, 17:33
par bastien83 » 24 Oct 2006, 17:33
maintenant il faut que j etudie le signe de f en fonction de x.
je sais que de ]-inf ;-1/2[f est -
en -1/2 f=0
et de ]-1/2;+inf[ f est+
mais comment je peut le demontrer etant donnée que je connais pas y (la tangente) ??
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 24 Oct 2006, 17:40
par Zebulon » 24 Oct 2006, 17:40
bastien83 a écrit:maintenant il faut que j etudie le signe de f en fonction de x.
je sais que de ]-inf ;-1/2[f est -
en -1/2 f=0
et de ]-1/2;+inf[ f est+
mais comment je peut le demontrer etant donnée que je connais pas y (la tangente) ??
Pourquoi avoir besoin de la tangente? Il suffit de résoudre
\geq0)
.
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 24 Oct 2006, 17:46
par bastien83 » 24 Oct 2006, 17:46
exacte.
on fait tellement de chose que l'on oublie de faire les choses toutes simples.
^^
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 24 Oct 2006, 17:47
par bastien83 » 24 Oct 2006, 17:47
petite question
0 est il + ou -????
car 0=-0
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 24 Oct 2006, 17:58
par Zebulon » 24 Oct 2006, 17:58
0 est positif et négatif.
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 24 Oct 2006, 18:30
par bastien83 » 24 Oct 2006, 18:30
je dois trouver une tangente t qui passe par le point B d'abscisse 1/2.
comment je fais.
je pense plutot remplacer lex x par 1/2 mais mes e^x vont un peu m'embeter dc je ne pense pas que ce soit la bonne soultion
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 24 Oct 2006, 18:46
par Zebulon » 24 Oct 2006, 18:46
La tangente à la courbe passant par le point d'abscisse

a pour équation
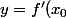x+f(x_0)-x_0.f'(x_0))
.
D'où ça sort?
1). On sait que c'est une droite donc son équation est de la forme y=ax+b.
2). Elle est tangente à la courbe au point
))
donc
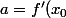)
.
3). Elle passe par
))
donc b vérifie
=f'(x_0).x_0+b)
donc
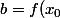-x_0.f'(x_0))
.
Donc ici?
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 25 Oct 2006, 12:41
par bastien83 » 25 Oct 2006, 12:41
on a f(1/2)-1/2*f'(1/2)
bizarre j'aurait plutot dis
t=f'(1/2)-(x-1/2)+f(1/2)
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 25 Oct 2006, 12:49
par Quidam » 25 Oct 2006, 12:49
Zebulon et Imod, vous êtes de valeureux guerriers ! Vous avez droit à tout mon respect et à toute mon admiration ! Vingt fois sur le métier..., et sans jamais perdre courage ! Quelle abnégation !
Si, si ! Sans rire ! Je n'aurais pas cette patience infinie !
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 25 Oct 2006, 12:55
par bastien83 » 25 Oct 2006, 12:55
Quidam a écrit:Zebulon et Imod, vous êtes de valeureux guerriers ! Vous avez droit à tout mon respect et à toute mon admiration ! Vingt fois sur le métier..., et sans jamais perdre courage ! Quelle abnégation !
Si, si ! Sans rire ! Je n'aurais pas cette patience infinie !
qu'est ce que tu sous entend que mon post precedent est une connerie^^.
En tout cas c'est vrai que ce sont de valeurreux guerriers.heureusement qu'ils sont la
:++:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Oct 2006, 13:20
par Zebulon » 25 Oct 2006, 13:20
Avez-vous compris ceci :
Zebulon a écrit:La tangente à la courbe passant par le point d'abscisse

a pour équation
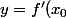x+f(x_0)-x_0.f'(x_0))
.
D'où ça sort?
1). On sait que c'est une droite donc son équation est de la forme y=ax+b.
2). Elle est tangente à la courbe au point
))
donc
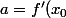)
.
3). Elle passe par
))
donc b vérifie
=f'(x_0).x_0+b)
donc
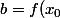-x_0.f'(x_0))
.
Pourquoi ce serait plutôt :
bastien83 a écrit:t=f'(1/2)-(x-1/2)+f(1/2)
?
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 25 Oct 2006, 13:27
par bastien83 » 25 Oct 2006, 13:27
Zebulon a écrit:Avez-vous compris ceci :
Pourquoi ce serait plutôt :
?
car l'equation d'une tangente est f'(a)(x-a)+f(a)
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Oct 2006, 13:52
par Zebulon » 25 Oct 2006, 13:52
Je suis d'accord. Ce n'est donc pas
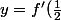-(x-{1\over2})+f({1\over2}))
!
Vous remarquerez que votre "formule", celle que vous sortez de votre cahier, est la même que la mienne, à la factorisation près.
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 25 Oct 2006, 13:56
par bastien83 » 25 Oct 2006, 13:56
donc pour calculer ma tangente, je calcule votre equation:
-1/2\times f'(1/2))
c'est exacte
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Oct 2006, 14:13
par Zebulon » 25 Oct 2006, 14:13
Grrr... Mais ce n'est pas ça mon équation !
C'est
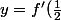(x-{1\over2})+f({1\over2}))
. Maintenant, il n'y a plus qu'à remplacer.
Combien vaut
)
? (vous devriez connaître la réponse sans même faire les calculs)
Combien vaut
)
?
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 25 Oct 2006, 14:20
par bastien83 » 25 Oct 2006, 14:20
ahhh je comprend mieux .c'est votre post num 34 qui m'a mis le doute sur la fonction car vous avez dit:
ce n'est donc pas.....
la je comprend
f(1/2)=0
f'(1/2)=0
??????,
y=0 c'ets bizarre :hum:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Oct 2006, 14:28
par Zebulon » 25 Oct 2006, 14:28
bastien83 a écrit:f'(1/2)=0
Qu'est-ce que vous trouvez comme dérivée de f?
-
bastien83
- Membre Relatif
- Messages: 376
- Enregistré le: 24 Sep 2006, 09:10
-
 par bastien83 » 25 Oct 2006, 14:30
par bastien83 » 25 Oct 2006, 14:30
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
a pour équation
.
donc
.
donc b vérifie
donc
.
