Bonjour à tous,
Je ne parviens pas à trouver la demarche pour passer de :
x^4 - 2(x^2)
à
x^4(1-(2/(x^2))
J ai cherché du coté de la factorisation de polynomes bicarrés mais sans résultat, il doit me manquer des connaissances.
Bien à vous.
Problème de factorisation
3 messages
- Page 1 sur 1
Re: Problème de factorisation
par Ben314 » 23 Jan 2017, 22:05
Salut,
Faut plutôt aller chercher du coté de la simplification de fractions vue au collège :
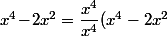=x^4\!\!\times\!\!\dfrac{x^4-2x^2}{x^4}=x^4\Big(\dfrac{x^4}{x^4}-\dfrac{2x^2}{x^4}\Big)=x^4\Big(1-\dfrac{2x^2}{x^2\!\times\!x^2}\Big)=x^4\Big(1-\dfrac{2}{x^2}\Big))
Et évidement, il faut bien préciser qu'on suppose
non nul pour que ça ait du sens.
Faut plutôt aller chercher du coté de la simplification de fractions vue au collège :
Et évidement, il faut bien préciser qu'on suppose
Modifié en dernier par Ben314 le 23 Jan 2017, 22:08, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :