Problème coordonées
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
timecrisis
- Membre Relatif
- Messages: 123
- Enregistré le: 09 Oct 2006, 18:08
-
 par timecrisis » 31 Jan 2007, 18:15
par timecrisis » 31 Jan 2007, 18:15
Soit ABC un triangle quelconque. On place le point P symétrique de A par rapport à B, le point Q symétrique de B par rapport a C et le point R symétrique de C apr rapport à A. On appelle I le milieu de [BC] et K le milieu de [PQ]. On appelle G et H les centres de gravité des triangles ABC rt PQR. on choisit le repere (A;AB;AC) (ce sont des vecteurs).
1) Determiner les coordonnées des points A,B,C==>c'est fait : A(0;0) B(1;0) C(0;1)
2) Déterminer les coordonnées du point I, puis celle de G ===> j'ai trouvé I(1/2;1/2) mais je ne sais pas comment faire pour trouver celles de G?
3)Déterminer les coordonnées des points R,P,Q et K
4)Démontrer que les points G et H sonts confondus.
Voila , j'ai réussi a faire la question 1 et un petit peut de la 2 pouvez-vous m'aider pour la suite. Merci
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 31 Jan 2007, 18:25
par Quidam » 31 Jan 2007, 18:25
timecrisis a écrit:mais je ne sais pas comment faire pour trouver celles de G?
G, centre de gravité du triangle ABC, est donc le barycentre de (A;1),(B;1),(C;1) ! Profite de l'aubaine !
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 31 Jan 2007, 19:06
par annick » 31 Jan 2007, 19:06
Bonsoir,
Tes premiers résultats sont justes. Je ne mets pas les vecteurs, mais ils y sont
GA+GB+GC=0
Exprime grâce à Chasles GB et GC en fonction de GA,AB,AC et tu obtiendras l'espression de AG en fonction de AB et AC, ce qui te permettra de trouver les coordonnées de G dans ton repère
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 31 Jan 2007, 19:20
par Quidam » 31 Jan 2007, 19:20
annick a écrit:Bonsoir,
GA+GB+GC=0
Exprime grâce à Chasles GB et GC en fonction de GA,AB,AC et tu obtiendras l'espression de AG en fonction de AB et AC, ce qui te permettra de trouver les coordonnées de G dans ton repère
GA+GB+GC=0 Certes ! Mais aussi :
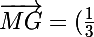[\vec{MA}+\vec{MB}+\vec{MC}])
quel que soit M et en particulier pour M=A :
[\vec{AA}+\vec{AB}+\vec{AC}]=(\frac{1}{3})\vec{AB}+(\frac{1}{3})\vec{AC})
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 31 Jan 2007, 19:54
par annick » 31 Jan 2007, 19:54
je suis d'accord avec toi Quidam, mais j'ai tendance à toujours repartir de la définition première du barycentre car je pense que c'est celle qui reste quand on a tout oublié.
-
timecrisis
- Membre Relatif
- Messages: 123
- Enregistré le: 09 Oct 2006, 18:08
-
 par timecrisis » 31 Jan 2007, 21:00
par timecrisis » 31 Jan 2007, 21:00
Quidam a écrit:G, centre de gravité du triangle ABC, est donc le barycentre de (A;1),(B;1),(C;1) ! Profite de l'aubaine !
tu peux ecrire les coordonnées correctoment car je ne comprend pas vraiment
-
timecrisis
- Membre Relatif
- Messages: 123
- Enregistré le: 09 Oct 2006, 18:08
-
 par timecrisis » 31 Jan 2007, 21:02
par timecrisis » 31 Jan 2007, 21:02
annick a écrit:Bonsoir,
Tes premiers résultats sont justes. Je ne mets pas les vecteurs, mais ils y sont
GA+GB+GC=0
Exprime grâce à Chasles GB et GC en fonction de GA,AB,AC et tu obtiendras l'espression de AG en fonction de AB et AC, ce qui te permettra de trouver les coordonnées de G dans ton repère
VOus pouvez m'epingler un petit peu car je ne vois pas comment et par quoi je pourrai commencer
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 31 Jan 2007, 21:18
par Quidam » 31 Jan 2007, 21:18
timecrisis a écrit:tu peux ecrire les coordonnées correctoment car je ne comprend pas vraiment
J'ai tout expliqué dans mon message de 19H20 ! Tu lis mes réponses ou pas ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
