Problème d'algèbre.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
ETINCELLE19
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Déc 2018, 12:33
-
 par ETINCELLE19 » 12 Fév 2019, 19:34
par ETINCELLE19 » 12 Fév 2019, 19:34
Bonsoir à tous, pouvez-vous m'aider à résoudre ce problème ?
Merci 
.
Soient

et

deux nombres réels distincts tels que
^{2})
et
^{2})
.
Calculer la valeur du nombre :
^{2018})
.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 12 Fév 2019, 19:47
par Carpate » 12 Fév 2019, 19:47
 \ x+1= (y-1)^2\\(2) \ y+1=(x-1)^2<br />\end{array})
Calcule (1) +(2) et (1) - (2)
Sauf erreur de ma part , on arrive à :
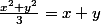
(x+y+3) = 0)
-
ETINCELLE19
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Déc 2018, 12:33
-
 par ETINCELLE19 » 12 Fév 2019, 20:09
par ETINCELLE19 » 12 Fév 2019, 20:09
Salut, j'ai ici :
+(2) } x^{2}+y^{2}=3(x+y) \\ <br /> & \text{ (1)-(2) } x^{2}-y^{2}=x-y <br />\end{cases})
J'ai trouvé
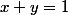
donc
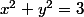
. Merci beaucoup

.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités