Pb probabilités : ramener le taux de réussite de 3 jets de d

[Korrigan]

Bonjour/Bonsoir,


Voilà 3 plombes que je cherche la solution à un problème... Ça me tape sur le système ! :mur:

En fait, c'est pour un jeu de rôle sur table. J'aimerais savoir comment ramener le pourcentage de réussite de plusieurs jets de dés d'affilé à un seul jet de dé.

Par exemple :

Un personnage a 30% de chance de réussir une action. Le joueur lance 2 dés à 10 faces (pour simuler un dé de 100, un dé faisant représentant le chiffre des dizaines, l'autre les unités). Le joueur doit alors faire au moins 30 pour réussir son action. Puis, il ré-éssait : à nouveau 30% de chance de réussite. Il essaie enfin une 3ème et dernière fois : toujours 30% de réussite.

La question est : Comment faire pour "ramener ces 3 jets de dés en un seul" (comme si le personnage n'effectuait qu'une seule action mais plus longue, durant 3 actions "de base" donc...), tout en gardant exactement le même taux de chance de réussite au final (c-a-d le même taux de chance de réussite en lançant 3 dés à la suite ou un seul) ???

OU, plus généralement et simplement, il me semble : Quelle est la probabilité de réussir 3 lancés à la suite ? (la formule permettant de calculer la probabilité de réussir AU MOINS UN lancé parmi plusieurs m'intéresse aussi...)


Merci infiniement à celui qui saura éclairer ma lanterne...

[Goux]

Le but est-il de réussir les trois lancés ?

Dans ce cas en faisant un arbre on peut facilement éclairer le problème et ainsi la probabilité de valider les 3 à la suite serait de 0.3^3

[hammana]

Bonjour/Bonsoir,


Voilà 3 plombes que je cherche la solution à un problème... Ça me tape sur le système ! :mur:

En fait, c'est pour un jeu de rôle sur table. J'aimerais savoir comment ramener le pourcentage de réussite de plusieurs jets de dés d'affilé à un seul jet de dé.

Par exemple :
Un personnage a 30% de chance de réussir une action. Le joueur lance 2 dés à 10 faces (pour simuler un dé de 100, un dé faisant représentant le chiffre des dizaines, l'autre les unités). Le joueur doit alors faire au 30 pour réussir son action. Puis, il ré-éssait : à nouveau 30% de chance de réussite. Il essaie enfin une 3ème et dernière fois : toujours 30% de réussite. Comment faire pour "ramener ces 3 jets de dés en un seul" (comme si le personnage n'effectuait qu'une seule action mais plus longue, durant 3 actions "de base" donc...), tout en gardant exactement le même taux de chance de réussite au final (c-a-d le même taux de chance de réussite en lançant 3 dés à la suite ou un seul) ???


Merci infiniement à celui qui saura éclairer ma lanterne...

Tu peux considérer 3 essais successifs comme une seule opération complexe pouvant conduire à 8 résultats différents. S désignnant un succès et E un échec, tu peux avoir:
SSS, SSE, SES, SEE, ESS, ESE, EES, EEE
Il y a une chance sur 8 d'avoir 3 succès,
3 sur 8 pour 2 succès,
3 sur 8 pour 1 succès et
1 sur 8 pour 3 échecs
et tu vérifies que 1/8+3/8+3/8+1/8=1

[Korrigan]

Merci pour cette réponse aussi rapide !

Pardon, c'est vrai que j'ai oublié de préciser : le but serait plutôt de réussir les 3 lancers mais la formule permettant de calculer la probabilité de réussir le lancer d'au moins 1 dé m'intéresserait aussi...

J'ai également édité mon post en précisant que les dés étaient des dés de 100 (simulés par 2 dés de 10 avec un dé représentant le chiffre des dizaines et l'autre les unités). Ça ne change rien au problème général mais je pense que ce n'était pas très clair...

Sinon, pour en venir à ta réponse, Goux : Un arbre de probabilités pourrait peut-être m'aider à résoudre le problème mais en fait c'est surtout la formule de calcul que j'aimerais trouver... Parce que faire un arbre de proba avec des dés de 100 ==> :cry: Et même en simplifiant et en prenant des dés de 10, si je désire ramener à un seul jet de dé le taux de réussite de 10 ou 20 lancés à la suite, je ne pourrai pas faire un arbre...

Désolé si je m'explique mal mais à vrai dire, j'ai moi-même du mal à visualer le problème... Erf... Mes cours de proba sont loin...

[Korrigan]

Pas d'autres réponses ? :triste:

[Luc]

Pas d'autres réponses ? :triste:

Si mais il faut que tu précises a quel condition tu considères que le lancé qui simule 3 lancers successifs est réussi. Est-ce que tu considère la réussite du "grand lancé" comme équivalente a la réussite aux trois "petits lancers" ou a au moins l'un des trois?

Si c'est le premier cas, alors les chances de succès sont (30/100)^3=0,027, soit a peu près 3 % : c'est peu!
Si c'est le deuxième cas, alors les chances de succès sont 1-(70/100)^3=0,657, soit a peu près 66% : c'est beaucoup plus!

La question naturelle derrière tout çà est la suivante : si tu lances n fois le couple de des a dix faces, avec une chance de succès toujours égale a 30/100, quelle est la probabilité d'avoir exactement k succès? Cette probabilité est la définition de la loi binomiale de paramètres n (nombre d’expérience) et 30/100 (probabilité de succès élémentaire) :
p( avoir k succès) =

[hammana]

Tu peux considérer 3 essais successifs comme une seule opération complexe pouvant conduire à 8 résultats différents. S désignnant un succès et E un échec, tu peux avoir:
SSS, SSE, SES, SEE, ESS, ESE, EES, EEE
Il y a une chance sur 8 d'avoir 3 succès,
3 sur 8 pour 2 succès,
3 sur 8 pour 1 succès et
1 sur 8 pour 3 échecs
et tu vérifies que 1/8+3/8+3/8+1/8=1

Je m'excuse, j'avais oublié que les chances de succès sont de 30%.
Il faut dire :
probabilité de 3 succès =(0.3)^3
2 sucès = 3*0.3^2*0.7
1 succès = 3*0.3*0.7^2
0 succès =0.7^3
Dans le cas général il faut appliquer la loi binomiale,









ç

[Korrigan]

Super ! Luc a parfaitement expliqué la problèmatique (mieux que moi en tout cas !). La question naturelle derrière tout ça est exactement celle que tu décris.

Par contre, il y a un truc qui me chagrine :

Bon, déjà, pour la probabilité de 3 succès d'affilé, on est tous d'accord. Mais concernant la probabilité d'un seul succès, ça me paraît bizarre. Luc, tu dis que les chances de succès sont 1-(70/100)^3=0,657, soit a peu près 66%. Seulement, si je m'en réfère à la loi binomiale que tu as toi-même écrit, soit :

\begin{pmatrix}
n \\
k
\end{matrix}

[Korrigan]

Super ! Luc a parfaitement expliqué la problèmatique (mieux que moi en tout cas !). La question naturelle derrière tout ça est exactement celle que tu décris.

Par contre, il y a un truc qui me chagrine :

Dans la loi binomiale écrite par Luc, je ne comprends pas à quoi correspond le premier terme, le "n k" entre parenthèses (désolé mais je n'arrive pas reproduire la notation mathématique). De plus, Hammana semble utiliser une formule de calcul différente puisque, lorsqu'il calcule la probabilité d'obtenir au moins 1 succès, il pose 3*0.3*0.7^2 et dans ce cas là, on trouve 0,441, soit environ 44%... tandis que Luc trouve (toujours pour au moins 1 succès) : 1-(70/100)^3=0,657, soit a peu près 66% ...

Vous n'êtes pas d'accord, on dirait ?

[Anonyme]

Voici quelques commentaires supplémentaires qui t'aideront peut-être à mieux comprendre les réponses précédentes

1) La loi binomiale permet de calculer la probabilité de l'événement "obtenir k succès" dans un schéma de Bernouilli à n épreuves.

2) La notation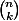 est le nombre de combinaison de k éléments dans un ensemble à n éléments (avec )
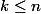ET on peut calculer ces nombres sur des calculatrices "niveau lycée"

3) Tu confonds les événements "obtenir 1 succès" et "obtenir au moins 1 succès"

4) Quand on veut calculer la probabilité de l'événement "obtenir au moins 1 succès" ,il est souvent plus simple de commencer par calculer la probabilité de l'événement contraire...

[Korrigan]

Okaaaay ! Je comprends mieux.

J'ai finalement trouvé la formule permettant de calculer ce fameux en cherchant un peu sur internet. Je vois mieux de quoi il s'agit maintenant. Et en effet, j'avais confondu les événements "obtenir pile poil 1 succès" et "obtenir au moins 1 succès". Les formules dont je parlais étaient donc différentes puisqu'elles ne calculaient pas du tout la même chose... Mais toutes sont justes. Enfin, ok pour le petit 4 : Calculer la probabilité d'obtenir au moins 1 succès revient à calculer la probabilité inverse de l'événement "ne pas obtenir le moindre succès".

Merci beaucoup pour vos réponses. Tout est clair maintenant !


[CENTER]--------------------------------------[/CENTER]


J'aimerais quand même poser 2 questions bonus... :langue2: Si personne n'y répond, ce n'est pas trop grave. C'est juste par curiosité :

1) Quelle serait la formule pour calculer la probabilité de l'événement "obtenir au moins 2 succès" ? Si j'ai bien compris, cela devait être égal à l'inverse de la probabilité de l'événement "n'obtenir que des ratés" + celle de l'événement "obtenir au moins 1 succès", soit :
1-(70/100)^3x[1-(70/100)^3] = 1-(0,7^3)x(1-0,7^3) = 1-(0,343x0,657) = 0,774649, soit environ 77%, ce qui me paraît pas mal...
J'ai juste ? Il n'y a pas une autre manière de calculer ce genre de probabilité, sans tout le temps passer par l'inverse ?

2) Comment cela se passe-t-il si les chances de succès changent d'un lancé à l'autre ? Par exemple :
Pour le premier lancé : faire 30%
Pour le deuxième lancé : faire 80%
Pour le troisième lancé : faire 50%

J'avais tout d'abord pensé à faire d'abord une moyenne de ces 3 pourcentages et utiliser ce nombre en tant que valeur pour k mais je pense que ce raisonnement est faux et archi-faux ...

[Anonyme]

Bonjour

Je te conseille maintenant que tu as compris ce qu'est la loi binomiale de prendre un bouquin de maths pour approfondir un peu plus ce sujet....
L'événement inverse n'existe pas il s'appelle "événement contraire"
Calculer la chance de.... s'appelle le calcul de la probabilité d'un événement

La probabilité d'un événement ne veut pas dire , comme tu l'as remarqué , que tu vas obtenir exactement ce résultat lors d'une expérimentation : ici on aborde un autre domaine qui s'appelle l'échantillonnage
Les notions à étudier/comprendre sur ce sujet, s'ils t'intéressent, sont :
fluctuation d'échantillonnage
intervalle de confiance à 95%
Simulation et estimation
Prise de décision
...etc...