Probabilité Variable aléatoire (urgent)
17 messages
- Page 1 sur 1
Probabilité Variable aléatoire (urgent)
Bonjour, j'ai besoin d'aide pour l'exercice suivant :
Lors de d'un jeu télévisé, les spectateurs peuvent jouer par sms. Il y a n cases (n supérieur ou égale a 4) numérotées de 1 a n.
Une case contient 10 euros, trois contiennent 5 euros et les autres 0 euro.
Le joueur envoie par sms le numéro d'une case et il gagne la somme correspondante.
On note X la variable qui compte le gain algébrique du joueur,.
On suppose que le coût du sms est de 1 euro.
a- Déterminez la loi de probabilité de la variable X.
b- Déterminez le gain moyen du joueur.
c- En déduire le nombre de case de valeur 0 euro a mettre pour que le jeu soit équitable (c'est-a-dire E(X)=0).
Pour ma part, j'en déduis que X est le gain déduit du coût de l'sms: si on envoie case 1 on gagne (-1+10=)9 euros, si on envoie cases 2, 3 et 4 on gagne (-1+5=) 4 euros et si on envoie case n on gagne (-1+0=)-1 euro. donc X peut prendre les valeurs {-1;4;9}. Ces valeurs correspondent a la première ligne du tableau de loi de la probabilité de X. Je sais que la somme des probabilités est égale a 1. Comment puis-je compléter la deuxième ligne si je ne connais la limite de n?
Lors de d'un jeu télévisé, les spectateurs peuvent jouer par sms. Il y a n cases (n supérieur ou égale a 4) numérotées de 1 a n.
Une case contient 10 euros, trois contiennent 5 euros et les autres 0 euro.
Le joueur envoie par sms le numéro d'une case et il gagne la somme correspondante.
On note X la variable qui compte le gain algébrique du joueur,.
On suppose que le coût du sms est de 1 euro.
a- Déterminez la loi de probabilité de la variable X.
b- Déterminez le gain moyen du joueur.
c- En déduire le nombre de case de valeur 0 euro a mettre pour que le jeu soit équitable (c'est-a-dire E(X)=0).
Pour ma part, j'en déduis que X est le gain déduit du coût de l'sms: si on envoie case 1 on gagne (-1+10=)9 euros, si on envoie cases 2, 3 et 4 on gagne (-1+5=) 4 euros et si on envoie case n on gagne (-1+0=)-1 euro. donc X peut prendre les valeurs {-1;4;9}. Ces valeurs correspondent a la première ligne du tableau de loi de la probabilité de X. Je sais que la somme des probabilités est égale a 1. Comment puis-je compléter la deuxième ligne si je ne connais la limite de n?
Re: Probabilité Variable aléatoire (urgent)
Bonjour
C'est un cas d'équiprobabilité donc (nombre d'issues favorables)/(nombre d'issues possibles)
Pour gagner 4 euros il y a 3 issues favorables et n issues possibles donc p(X=4)=3/n ce n'est pas plus compliqué que cela... ainsi de suite
C'est un cas d'équiprobabilité donc (nombre d'issues favorables)/(nombre d'issues possibles)
Pour gagner 4 euros il y a 3 issues favorables et n issues possibles donc p(X=4)=3/n ce n'est pas plus compliqué que cela... ainsi de suite
Re: Probabilité Variable aléatoire (urgent)
Merci pour votre aide. Donc, si j'ai bien compris : le nombre d'issues possibles correspond a n, ce qui fait que, en tenant compte de l'équiprobabilité, p(X=-1)=1/n, p(X=4)=3/n et p(X=9)=1/n. Comment être sur que la somme des probabilités vale 1? Et le gain moyen du joueur est E(X)= 1/n*(-1)+3/n*4+1/n*9. Est-ce bien cela ?
Re: Probabilité Variable aléatoire (urgent)
Bonjour,
Deux résultats sont corrects, l'un est incorrect.
La somme doit toujours faire 1. Et ici, votre somme est
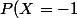+P(X=4)+P(X=9)=\dfrac{1}{n}+\dfrac{3}{n}+\dfrac{1}{n}=\dfrac{5}{n})
Ce qui n'est pas égal à 1 (sauf si n=5 mais ce n'est qu'un cas particulier) et doit vous alerter sur le fait qu'il y a bien une erreur dans la loi de probabilité.
La formule appliquée est correcte et le résultat deviendra correct quand la loi de probabilité sera corrigée. mais il ne faut pas la laisser telle quelle car on peut simplifier le résultat.
Question : combien y a-t-il de cases perdantes ?
AinaJ a écrit: p(X=-1)=1/n, p(X=4)=3/n et p(X=9)=1/n
Deux résultats sont corrects, l'un est incorrect.
AinaJ a écrit: Comment être sur que la somme des probabilités vale 1?
La somme doit toujours faire 1. Et ici, votre somme est
Ce qui n'est pas égal à 1 (sauf si n=5 mais ce n'est qu'un cas particulier) et doit vous alerter sur le fait qu'il y a bien une erreur dans la loi de probabilité.
AinaJ a écrit:Et le gain moyen du joueur est E(X)= 1/n*(-1)+3/n*4+1/n*9.
La formule appliquée est correcte et le résultat deviendra correct quand la loi de probabilité sera corrigée. mais il ne faut pas la laisser telle quelle car on peut simplifier le résultat.
Question : combien y a-t-il de cases perdantes ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Probabilité Variable aléatoire (urgent)
En effet quand tu écris
cela signifie qu'il y a une seule case perdante parmi les n cases et cela ne correspond pas à la réalité.
AinaJ a écrit:p(X=-1)=1/n
cela signifie qu'il y a une seule case perdante parmi les n cases et cela ne correspond pas à la réalité.
Re: Probabilité Variable aléatoire (urgent)
Si je réponds a la question : il y a n-4 cases perdantes. C'est bien ça ?
Re: Probabilité Variable aléatoire (urgent)
Ou plutôt p(X=-1)=1-(p(x=4)+p(X=9) ce qui équivaut a 1-(3/n+1/n) = 1-4/n. p(X=-1)=1-4/n. C'est cela ?
Re: Probabilité Variable aléatoire (urgent)
Bonjour, d'accord, merci pour votre aide. Donc, si je résume p(X=-1)=1-4/n, p(X=4)=3/n et p(X=9)=1/n. Le gain moyen du joueur est E(X)= (1-4/n)*(-1)+3/n*4+1/n*9. Est-ce correct ?
Re: Probabilité Variable aléatoire (urgent)
... Et à simplifier en mettant tout au même dénominateur (ce qui permet de répondre très facilement à la dernière question)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Probabilité Variable aléatoire (urgent)
Donc =-1(1-4/n)+4*3/n+9*1/n) ce qui fait
ce qui fait =-1+4/n+4/1*3/n+9/1*1/n) . Je trouve
. Je trouve =-n/n+4/n+12/n+9/n) soit
soit =(-n+4+12+9)/n) . J'ai mis le tout au même dénominateur mais je trouve quelque chose ne va pas dans mes opérations. Ou me suis-je tromper ? Je vois que pour répondre a la dernière question de l'exercice je dois aboutir a une résolution d’équation, c'est bien cela ?
. J'ai mis le tout au même dénominateur mais je trouve quelque chose ne va pas dans mes opérations. Ou me suis-je tromper ? Je vois que pour répondre a la dernière question de l'exercice je dois aboutir a une résolution d’équation, c'est bien cela ?
Re: Probabilité Variable aléatoire (urgent)
Oui c'est juste
Tu dois résoudre E(X)=0 d'inconnue n.
Rappel : Un quotient est nul si et seulement si son numérateur est nul
Tu dois résoudre E(X)=0 d'inconnue n.
Rappel : Un quotient est nul si et seulement si son numérateur est nul
Re: Probabilité Variable aléatoire (urgent)
Donc, =(-n+4+12+9)/n) ce qui fait
ce qui fait =(-n+25)/n) . Pour répondre a la question c), je fais
. Pour répondre a la question c), je fais =(-n+25)/n=0) , pourtant la propriété dit :"un quotient est nul si le numérateur est nul". Je trouve que le numérateur est différent de 0 et n est égal a un ensemble vide. Comment ça se fait ?
, pourtant la propriété dit :"un quotient est nul si le numérateur est nul". Je trouve que le numérateur est différent de 0 et n est égal a un ensemble vide. Comment ça se fait ?
Re: Probabilité Variable aléatoire (urgent)
Pour quelle valeur de n a-t-on : -n + 25 = 0 ?
C'est quand même pas compliqué, non ?
C'est quand même pas compliqué, non ?
Re: Probabilité Variable aléatoire (urgent)
Ah oui, c'est vrai, je suis désolée j'ai mal compris la propriété. On a -n+25=0 pour n=25, ce qui fait E(X)=21/25*(-1)+3/25*4+1/25*9=0. Le jeu est bien équitable pour 25 cases de 0 euro. Merci de votre aide et de votre patience.
Re: Probabilité Variable aléatoire (urgent)
Oui mais attention à la conclusion, n est le nombre total de cases, pas celui des cases perdantes.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 183 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
