Alors voila la souci c'est un exo qui porte sur les depistage de maladie mais il est pas vraiment comme dhabitude ...
On estime que sur 1000 personne 10 sont atteinte soit 1% de 1000 personnes... Pour tester on repartie les 1000 personnes dans n groupe de r personnes, on rassemble tout les test du même groupe, et un groupe est negatif lorsque aucun test est positif et donc un groupe est positif si au moins un test est positif ... Dans ce dernier ca on retest cas par cas les personne du groupe positif ...
Première question :
Quelle est la probabilité p qu'un groupe soit positif ... ?????
Pour le reste de l'éxercide ensuite je pense pouvoir m'en sortir mais la je ne comprend pas le principe ... Merci d'avance
Probabilité terminale S
7 messages
- Page 1 sur 1
Merci pour cette reponse rapide. Oui ca pourrai en effet être ca merci j'etait un peu parti la dessu seulement le reste de lexercice reste plutot difficile en partant comme cela. Les questions suivantes consistent à determiner la probabilité q qu'un groupe soit positif ...
soit q = 1 - p
Puis ensuite on pose Y la variable aleatoire donnant le nombre de groupe positif, il fau alor montrer que y repond a la loi binomiale de
paramètre ( n ; q ) et la j'avoue être un peu larguer ...
soit q = 1 - p
Puis ensuite on pose Y la variable aleatoire donnant le nombre de groupe positif, il fau alor montrer que y repond a la loi binomiale de
paramètre ( n ; q ) et la j'avoue être un peu larguer ...
slt en effet Y suit la loi binômiale de paramètre n, car il y a n groupe et que l'expèrience d'un tirage "o hasard" d'un groupe est reproduite n fois, alors la proba d'un succès est donnée par p=q=1-(r parmi 1000)/(r parmi 1000), et celle d'un échec (le groupe est négatif)=1-p=(r parmi 990)/(r parmi 1000), Y désigne le nombre de succès donc par définition p(Y=k)=(k parmi n)*(q)^k * (1-q)^(n-k), où n désigne le nombre de tirage d'un groupe ! @ +
En effet j'ai donné la proba de l'événement contraire.
Cependant avec cette interprétation le nombres de groupes positifs ne suit pas une loi binomiale : il y a au moins un groupe positif et les tirages ne sont pas indépendants.
On peut alors comprendre : on tire (dans une population pratiquement infinie) n groupes de r personnes.
La proba qu'un tel roupe soit positif est :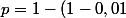^r) .
.
Le nombre aléatoire Y de goupes positif suit une loi B(n;p).
Cependant avec cette interprétation le nombres de groupes positifs ne suit pas une loi binomiale : il y a au moins un groupe positif et les tirages ne sont pas indépendants.
On peut alors comprendre : on tire (dans une population pratiquement infinie) n groupes de r personnes.
La proba qu'un tel roupe soit positif est :
Le nombre aléatoire Y de goupes positif suit une loi B(n;p).
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
