Je suis pas sûr qu'il y ait une construction explicite du (ou des)

et

du résultat vu que le seul truc qui me semble raisonnable comme preuve, ça utilise le "Principe des tiroirs" qui est essentiellement non constructif.
On suppose

et pose
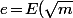\!\in\!{\mathbb N})
(partie entière) c'est à dire

.
Pour tout

, comme
\!=\!1)
l'équation (d'inconnus

et

)

admet une infinité de solutions de la forme

avec
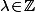
donc il existe (exactement) une solution
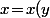\!\in\!\{0..m\!-\!1\})
.
De plus, si

et que
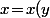)
et
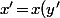)
alors

et

sont divisibles par

donc
\!-\!(y\!-\!y'))
l'est aussi et, vu que

n'est pas divisible par

(car

), on a forcément

, c'est à dire

.
Rangeons les

différents
)
dans l'ordre décroissant :

et notons

les

correspondant (qui sont les entiers

réécrits dans un certain ordre)
Si on pose

, on a :
M\leq (x_0\!-\!x_1)\!+\!(x_1\!-\!x_2)\!+...+\!(x_{e-1}\!-\!x_{e})\!+\!(m\!+\!x_e\!-\!x_0)=m<(e\!+\!1)^2)
Donc

ce qui signifie que

(car

et entier).
Deux cas se présentent alors :
- Soit il existe

tel que

et les entiers

et

sont tels que :

avec

est divisible par

.
- Soit

et les entiers

et

sont tels que :

avec

est divisible par

.