2) f(x)= ax+bx+c
donc f'(x) = a+b quelque soit x
DM pour demain
16 messages
- Page 1 sur 1
avec la correction d'énoncé qui va bien
1) quelle sont les fonctions qui ont une dérivée nulle ? Y en a til une seule ? non donc tu as un contreexemple.
2) tu calcules la dérivée de f, c'est à dire f'(x). puis après tu calcules f'(-b/2a) tu dois bien trouver 0.
3) la tangeante à une courbe d'équation f au point x0 est la droite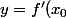x- f'(x_0) x_0+f(x_0))
tu calcules la fonction dérivée f' et tu identifies avec y=2x-1
tu doit trouver un x0 tq f'(x_0)=2 et -x_0 f'(x_0)+f(x_0)=-1
maf a écrit:2) f(x)= ax²+bx+c
donc f'(x) = 2ax+b quelque soit x
1) quelle sont les fonctions qui ont une dérivée nulle ? Y en a til une seule ? non donc tu as un contreexemple.
2) tu calcules la dérivée de f, c'est à dire f'(x). puis après tu calcules f'(-b/2a) tu dois bien trouver 0.
3) la tangeante à une courbe d'équation f au point x0 est la droite
tu calcules la fonction dérivée f' et tu identifies avec y=2x-1
tu doit trouver un x0 tq f'(x_0)=2 et -x_0 f'(x_0)+f(x_0)=-1
3) La droite d'équation y=2x-1 est-elle tangente à la courbe d'équation y=1/x en un point?
d'après moi, pour répondre à ta question, il faut se souvenir que le coefficient directeur de la tangente en un point d'une courbe est donné par la valeur de la dérivée en ce point.
Le coefficient directeur de la droite que l'on te donne est 2 car y=2x-1
La dérivée de ta fonction 1/x est
(1/x)'=-1/x²
Cherchons donc si -1/x² peut être égal à 2
d'après moi, pour répondre à ta question, il faut se souvenir que le coefficient directeur de la tangente en un point d'une courbe est donné par la valeur de la dérivée en ce point.
Le coefficient directeur de la droite que l'on te donne est 2 car y=2x-1
La dérivée de ta fonction 1/x est
(1/x)'=-1/x²
Cherchons donc si -1/x² peut être égal à 2
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
