DM: Positions relatives de deux courbes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 15 Sep 2013, 11:41
par mcar0nd » 15 Sep 2013, 11:41
Salut,
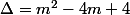
, ça ne te fait pas penser à une identité remarquable?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 15 Sep 2013, 11:51
par mcar0nd » 15 Sep 2013, 11:51
Médéric DIAO a écrit:Salut, donc V(delta)m = m-4 ok, merci

Mais comment prouver que si m>2, V(delta)m=m-2 ?
Il faut une inéquation je suppose mais je n'arrive pas à la trouver...
Attention,
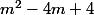
n'est pas égal à
^2)
.
Tu as fais une erreur en écrivant ton identité remarquable.
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 15 Sep 2013, 11:58
par mcar0nd » 15 Sep 2013, 11:58
Médéric DIAO a écrit:ah oui (m-2)^2 ok mais comment dire que c'est égale pour m>2?
^2)
s'annule en 2, ce que tu as trouvé.
Donc, quand x>2, tu as
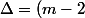^2 \Longleftrightarrow \sqrt{ \Delta}= \sqrt{ (m-2)^2} = m-2)
.
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 15 Sep 2013, 12:06
par mcar0nd » 15 Sep 2013, 12:06
Médéric DIAO a écrit:oui et dans ce cas comment ça marche pour V(delta)m=2-m, si m<2 ?
Pour x<2, m-2<0 ça c'est facile. Alors que
^2 } \gt 0)
donc il faut trouver une solution pour que m-2 et
^2 })
soit de même signe.
POur ça on prend l'opposé de m-2, soit -(m-2)=-m+2=2-m.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
