PGCD (arithmétique des entiers)

[charly45]

Bonjours,
J'ai un exercice de spécialité dans lequel je patauge.

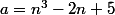
Soit n IN, et b=n+1.
A) Montrer que PGCD(a,b)=PGCD(b,6).
B) Pour quelle valeur de n a-t-on PGCD(a,b)=3 ?
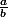
C) Déterminer n pour que le nombre soit un entier relatif.

Pouvez-vous m'aider ?

[Ericovitchi]

Ca donne envie de voir ce que donne la division de a par b et donc d'écrire
n^3-2n+5 = (n+1)(n²-n-1) + 6

le PGCD de a et b divise le membre de gauche et aussi (n+1) à droite donc il divise 6, etc...

[charly45]

Merci Ericovitchi.

Pour le B) j'ai fait :
6=3x1+3
3=3x1+0
On prend le dernier reste non nul, donc on en conclut que PGCD(6,3)=3
Donc lorsque n vaut 3, on a PGCD(a,b)=3.

Cela est-il juste ?