Petite question à propos de Delta.
6 messages
- Page 1 sur 1
Petite question à propos de Delta.
par Littl3-n4nyZz » 12 Oct 2007, 19:56
Ca va j'ai résolu mon truc, pas la peine de m'hurler dessus :-)
par le_fabien » 12 Oct 2007, 20:08
salut
je vois pas ce que tu veux calculer mais je sais que "delta" ne se calcule que pour des polynômes du second degré comme par ex 2x^2-3x+7
je vois pas ce que tu veux calculer mais je sais que "delta" ne se calcule que pour des polynômes du second degré comme par ex 2x^2-3x+7
par le_fabien » 12 Oct 2007, 20:15
aide moi et dis moi ce que tu veux faire avec cette fonction et si je peux je t'aiderais
par Quidam » 12 Oct 2007, 20:38
C'est quoi Delta ? Pour moi c'est une lettre grecque ! Alors, désolé, mais calculer Delta tout seul, ça ne veut strictement rien dire !
C'est comme si tu demandais si on peut calculer r ou s ou w !
C'est vrai, je fais semblant de ne pas comprendre ! Ce n'est pas la première fois que j'entends ce genre de question ! Il en est même qui demandent "peut-on FAIRE DELTA ?" !!!
Dans la résolution d'une équation du second degré, ou dans la factorisation d'un trinôme du second degré on est amené à calculer le discriminant de cette équation, ou de ce trinôme. Il se trouve, effectivement, qu'il est d'usage de donner à ce discriminant le nom Delta ! Mais rien n'empêcherait de l'appeler w ou z ! Alors, je t'en prie, désormais, tu pourras parler de Delta après et seulement après l'avoir défini, par une phrase comme : "soit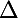
le discriminant de ce trinôme" parce que parler de Delta sans l'avoir défini, ça n'a pas de sens !
Cela dit, à ma connaissance, le seul cas dans le programme du lycée où l'on doit calculer un discriminant est celui d'un trinôme du second degré dont on cherche les racines.
[CENTER]Peut-on calculer Delta dans une fraction?[/CENTER]
Le "Delta" d'une fraction, tu ne sais pas ce que c'est ! Le discriminant d'une fraction, pas davantage ! Alors la question du calcul du discriminant d'une fraction ne se pose même pas : on ne sait pas ce que c'est !
Par contre, le numérateur de cette fraction est effectivement un trinôme du second degré. Alors, rien ne t'empêche de calculer son discriminant, mais la question est : que vas-tu en faire une fois que tu l'auras calculé ! Le discriminant sert à trouver les racines du trinôme. Calculer le discriminant du numérateur ici, pourrait servir à trouver les solutions de f(x)=0
Alors, si tu souhaites chercher les solutions de f(x)=0, tu peux effectivement calculer le discriminant ! Mais il y a plus simple : sans calculer le discriminant, on voit immédiatement que le numérateur de cette fraction n'a pas de racine. Et de toutes façons, trouver les racines (s'il y en a) du numérateur ne sert à rien si tu es en train de vérifier une tangente ! Pour trouver l'équation d'une tangente, il faut calculer la dérivée f '(x) : le discriminant, les racines du numérateur, ne servent à rien pour calculer f '(x) !
Dernier point, et non le moindre !
En première on apprend à résoudre toutes les équations du type ax²+bx+c=0. Mais il ne faut pas oublier qu'il y a des cas particuliers de l'équation du second degré que l'on sait résoudre bien avant la première, bien avant d'apprendre ce qu'est un discriminant !
Premier cas : b=0
ax²+c=0 On résoud cela en troisième :
Exemple x²-4=0 ! On apprend en troisième à factoriser grâce à l'identité remarquable a²-b²=(a+b)*(a-b). Effectivement :
x²-4 =0 équivaut à (x-2)*(x+2)=0 d'où les deux solutions x=2 et x=-2 !
Autre exemple : x²+5 = 0 ! En troisième on sait déjà que cette équation n'a pas de solution, puisque
et que par conséquent 
! Il est donc impossible que ça fasse 0 !
Deuxième cas : c=0
ax²+bx=0 On résoud cela en troisième également ! Car x est un facteur évident !
Exemple : 2x²-7x = 0
est équivalent à x*(2x-7)=0 ce qui conduit aux deux solutions x=0 et x=7/2 !
Par conséquent, il est absurde de calculer le discriminant lorsque l'on est dans l'un de ces deux cas simples !
La seule nouveauté de la première est de savoir résoudre ax²+bx+c=0 même dans le cas où aucun des trois coefficients a, b et c n'est nul ! Alors, si tu veux chercher les racines de ton numérateur, "2x²+6", un petit peu de réflexion t'amènera à la conclusion immédiate que ce numérateur n'a pas de racine ! Si tu calcules quand même le discriminant, tu trouveras un nombre négatif !
Ah, j'ai failli oublier :
Je suppose que Cf est la courbe représentative de f (encore un truc que tu n'as pas défini !). Alors étant donné que Cf est une courbe qui n'est pas une droite, je ne vois pas comment Cf pourrait être parallèle à une droite !
C'est comme si tu demandais si on peut calculer r ou s ou w !
C'est vrai, je fais semblant de ne pas comprendre ! Ce n'est pas la première fois que j'entends ce genre de question ! Il en est même qui demandent "peut-on FAIRE DELTA ?" !!!
Dans la résolution d'une équation du second degré, ou dans la factorisation d'un trinôme du second degré on est amené à calculer le discriminant de cette équation, ou de ce trinôme. Il se trouve, effectivement, qu'il est d'usage de donner à ce discriminant le nom Delta ! Mais rien n'empêcherait de l'appeler w ou z ! Alors, je t'en prie, désormais, tu pourras parler de Delta après et seulement après l'avoir défini, par une phrase comme : "soit
Cela dit, à ma connaissance, le seul cas dans le programme du lycée où l'on doit calculer un discriminant est celui d'un trinôme du second degré dont on cherche les racines.
[CENTER]Peut-on calculer Delta dans une fraction?[/CENTER]
Le "Delta" d'une fraction, tu ne sais pas ce que c'est ! Le discriminant d'une fraction, pas davantage ! Alors la question du calcul du discriminant d'une fraction ne se pose même pas : on ne sait pas ce que c'est !
Par contre, le numérateur de cette fraction est effectivement un trinôme du second degré. Alors, rien ne t'empêche de calculer son discriminant, mais la question est : que vas-tu en faire une fois que tu l'auras calculé ! Le discriminant sert à trouver les racines du trinôme. Calculer le discriminant du numérateur ici, pourrait servir à trouver les solutions de f(x)=0
Alors, si tu souhaites chercher les solutions de f(x)=0, tu peux effectivement calculer le discriminant ! Mais il y a plus simple : sans calculer le discriminant, on voit immédiatement que le numérateur de cette fraction n'a pas de racine. Et de toutes façons, trouver les racines (s'il y en a) du numérateur ne sert à rien si tu es en train de vérifier une tangente ! Pour trouver l'équation d'une tangente, il faut calculer la dérivée f '(x) : le discriminant, les racines du numérateur, ne servent à rien pour calculer f '(x) !
Dernier point, et non le moindre !
En première on apprend à résoudre toutes les équations du type ax²+bx+c=0. Mais il ne faut pas oublier qu'il y a des cas particuliers de l'équation du second degré que l'on sait résoudre bien avant la première, bien avant d'apprendre ce qu'est un discriminant !
Premier cas : b=0
ax²+c=0 On résoud cela en troisième :
Exemple x²-4=0 ! On apprend en troisième à factoriser grâce à l'identité remarquable a²-b²=(a+b)*(a-b). Effectivement :
x²-4 =0 équivaut à (x-2)*(x+2)=0 d'où les deux solutions x=2 et x=-2 !
Autre exemple : x²+5 = 0 ! En troisième on sait déjà que cette équation n'a pas de solution, puisque
Deuxième cas : c=0
ax²+bx=0 On résoud cela en troisième également ! Car x est un facteur évident !
Exemple : 2x²-7x = 0
est équivalent à x*(2x-7)=0 ce qui conduit aux deux solutions x=0 et x=7/2 !
Par conséquent, il est absurde de calculer le discriminant lorsque l'on est dans l'un de ces deux cas simples !
La seule nouveauté de la première est de savoir résoudre ax²+bx+c=0 même dans le cas où aucun des trois coefficients a, b et c n'est nul ! Alors, si tu veux chercher les racines de ton numérateur, "2x²+6", un petit peu de réflexion t'amènera à la conclusion immédiate que ce numérateur n'a pas de racine ! Si tu calcules quand même le discriminant, tu trouveras un nombre négatif !
Ah, j'ai failli oublier :
Littl3-n4nyZz a écrit:En fait, c'est pour vérifier s'il y a ou non une tangente parallèle à Cf...
Je suppose que Cf est la courbe représentative de f (encore un truc que tu n'as pas défini !). Alors étant donné que Cf est une courbe qui n'est pas une droite, je ne vois pas comment Cf pourrait être parallèle à une droite !
par anima » 12 Oct 2007, 21:01
Priere de ne pas cliquer sur le petit panneau "attention" pour rien, Littl3-n4nyZz. Quidam a parfaitement raison sur tous les plans, et n'a pas été méchant.
(Y'a que la vérité qui blesse)
(Y'a que la vérité qui blesse)
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :