Bonsoir, j'aurais besoin d'une petite explication...( je travaille sur les nombres complexes et on souhaite établir un surcorps de R, c'est le contexte..)
on appelle (a',b') l'élément symétrique s'il existe et j'ai (a,b).(a',b')=(aa'-bb',ab'+ba')=(1,0) (1,0) qui est en fait l'élément neutre.
Voilà on doit montrer qu'il existe des éléments symétriques.
on a donc:
aa'-bb'=1
ab'+ba'=0
mais je ne comprends pas la suite de la démonstration..
|a -b|
|b a|
a²+b² , différent de 0
donc le système admet une solution unique d'où tout élément admet un symétrique
j'ai pa compris...., veuillez m'éclaircir svp.
Bonne soirée.
Petite question (élément symétrique)
3 messages
- Page 1 sur 1
Je sais pas mais on peut faire comme ça
si on considere l'element (a,b) non nul
L'inverse est)
EDIT: j'ai crompris finalement
On veut résoudre le systeme

d'inconnues a',b' dans R
Le determinant de ce systeme vaut a²+b² et est donc pas nul.
En conséquence le systeme est inversible, le systeme a une unique solution.
Si tu préfére le point de vu matriciel:
On veut résoudre l'equation suivante d'inconnue

Le determinant de la matrice vaut a²+b², la matrice est inversible.
L'equation a une unique solution
Sinon on résout carémment le systeme

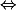
\times b'&=&-\frac{b}{a}&\quad L_{2} \leftarrow L_{2}-\frac{b}{a}L_{1}\end{array})
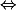

si on considere l'element (a,b) non nul
L'inverse est
EDIT: j'ai crompris finalement
On veut résoudre le systeme
d'inconnues a',b' dans R
Le determinant de ce systeme vaut a²+b² et est donc pas nul.
En conséquence le systeme est inversible, le systeme a une unique solution.
Si tu préfére le point de vu matriciel:
On veut résoudre l'equation suivante d'inconnue
Le determinant de la matrice vaut a²+b², la matrice est inversible.
L'equation a une unique solution
Sinon on résout carémment le systeme
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
