bonjour, j'aurai besoin de quelques inormations sur un exo de vecteurs, que je n'arrive pas à faire, alors l'exo c'est dans un repère (A;vAB;vAC), ABC est un triangle quelconque et A' est le milieu de BC, B' milieu de CA et C' milieu de AB.
M est le milieu de BC' et L est symétrique de A' par àB, il faut que je détermine tous les coordonnées de tous les points, et de montrer que B', M et L sont alignés, aidez oi svp :help:
Un petit pb de vecteurs
7 messages
- Page 1 sur 1
Ne sait tu pas écrire avec des vecteurs que :
"L est symétrique de A' par rapport à B"
Plus précisément, quel lien y a-t-il entre las vecteurs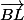 et
et 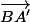 ?
?
Peut tu calculer les coordonnées d'un de ces deux vecteurs ?
En déduire celles de l'autre ?
.
.
.
"L est symétrique de A' par rapport à B"
Plus précisément, quel lien y a-t-il entre las vecteurs
Peut tu calculer les coordonnées d'un de ces deux vecteurs ?
En déduire celles de l'autre ?
.
.
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
