Petit question
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mari2
- Membre Relatif
- Messages: 268
- Enregistré le: 14 Nov 2007, 00:06
-
 par mari2 » 14 Jan 2009, 21:37
par mari2 » 14 Jan 2009, 21:37
Bonjour je voudrai savoir si quelqu'un pouvait me dire la suite de cette démonstration.
e^io=coso+isino (o=théta)
et pour tout réel o et o', e^io*e^io'=e^i(o+o')
En déduire que pour tout n de N,
(e^io)^n=e^ino
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 14 Jan 2009, 21:51
par Clembou » 14 Jan 2009, 21:51
mari2 a écrit:Bonjour je voudrai savoir si quelqu'un pouvait me dire la suite de cette démonstration.
e^io=coso+isino (o=théta)
et pour tout réel o et o', e^io*e^io'=e^i(o+o')
En déduire que pour tout n de N,
(e^io)^n=e^ino
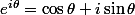
c'est la formule d'Euler :
http://fr.wikipedia.org/wiki/Formule_d'Euler 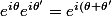})
cela vient de la fonction exponentielle.
Ensuite, tu peux facilement déduire le reste... :++:
-
mari2
- Membre Relatif
- Messages: 268
- Enregistré le: 14 Nov 2007, 00:06
-
 par mari2 » 14 Jan 2009, 22:05
par mari2 » 14 Jan 2009, 22:05
En fait j'ai trouvé la démonstration mais je n'arrive pas à en déduire la formule qu'il demande alors que je suis sur que c'est super simple ^^ .
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 14 Jan 2009, 22:08
par Clembou » 14 Jan 2009, 22:08
mari2 a écrit:En fait j'ai trouvé la démonstration mais je n'arrive pas à en déduire la formule qu'il demande alors que je suis sur que c'est super simple ^^ .
La formule de Moivre (avec les puissances n).
Pourquoi ne pas dire que :


fois ?
-
mari2
- Membre Relatif
- Messages: 268
- Enregistré le: 14 Nov 2007, 00:06
-
 par mari2 » 14 Jan 2009, 22:13
par mari2 » 14 Jan 2009, 22:13
oui la formule de moivre je la connais mais je comprend pas ce que je doit faire avec ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 14 Jan 2009, 22:15
par Clembou » 14 Jan 2009, 22:15
mari2 a écrit:oui la formule de moivre je la connais mais je comprend pas ce que je doit faire avec ?
Tu dois montrer que :
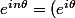^n)
mais tu sais que :

-
mari2
- Membre Relatif
- Messages: 268
- Enregistré le: 14 Nov 2007, 00:06
-
 par mari2 » 14 Jan 2009, 22:20
par mari2 » 14 Jan 2009, 22:20
e^io*e^io'=e^i(o+o')
<=> (coso+isino)^n=cos(no)+(isin(no)
<=>(e^io)^n=e^ino
C'est ça que je dois faire ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 14 Jan 2009, 22:22
par Clembou » 14 Jan 2009, 22:22
mari2 a écrit:e^io*e^io'=e^i(o+o')
(coso+isino)^n=cos(no)+(isin(no)
(e^io)^n=e^ino
C'est ça que je dois faire ?
Moi j'aurais préféré celle-ci :
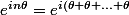} = ... = e^{i\theta}^n)
Maintenant, il faut compléter les trous avec la relation de l'exponentielle (deuxième formule)...
-
mari2
- Membre Relatif
- Messages: 268
- Enregistré le: 14 Nov 2007, 00:06
-
 par mari2 » 14 Jan 2009, 22:35
par mari2 » 14 Jan 2009, 22:35
(e^io)^n=e^i(o+o+...+o)=e^io*e^io'=e^(o+o')=e^ino
C'est bon ça ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 14 Jan 2009, 23:11
par Clembou » 14 Jan 2009, 23:11
Que vaut
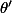
?
En fait pas la peine de passer par les
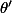
. Réfléchis bien !
-
mari2
- Membre Relatif
- Messages: 268
- Enregistré le: 14 Nov 2007, 00:06
-
 par mari2 » 14 Jan 2009, 23:13
par mari2 » 14 Jan 2009, 23:13
o' c'est arg(z') nan ?
(e^io)^n=e^i(o+o+...+o)=e^io*e^io*...*e^io=e^(o+o')=e^ino
C'est ça sans les o' ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 14 Jan 2009, 23:31
par Clembou » 14 Jan 2009, 23:31
mari2 a écrit:o' c'est arg(z') nan ?
(e^io)^n=e^i(o+o+...+o)=e^io*e^io*...*e^io=e^(o+o')=e^ino
C'est ça sans les o' ?
Oula ! Tu t'es emmelé les pinceaux :triste:
Pourquoi :
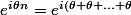})
?
C'est pas plutôt
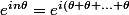})
?
-
mari2
- Membre Relatif
- Messages: 268
- Enregistré le: 14 Nov 2007, 00:06
-
 par mari2 » 14 Jan 2009, 23:44
par mari2 » 14 Jan 2009, 23:44
ha oui dsl jme suis trompé?
(e^ino)=e^i(o+o+...+o)=e^io*e^io*...*e^io=(e^io)^n
C'est bon maintenant ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 14 Jan 2009, 23:59
par Clembou » 14 Jan 2009, 23:59
Voilà ! Là, c'est bon :++:
-
mari2
- Membre Relatif
- Messages: 268
- Enregistré le: 14 Nov 2007, 00:06
-
 par mari2 » 15 Jan 2009, 00:09
par mari2 » 15 Jan 2009, 00:09
Merci pour ton aide.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
