Petit problème

[bastien83]

Bonsoir à tous,

Pourriez-vous m'aider à résoudre ce solution :

(e^x +1)(e^x-4) = 0


Merci d'avance

[Monsieur23]

Si un produit est nul, alors un des facteurs est nul.

Tu as donc deux cas à faire

Bon courage,
Mr.23

[Yawgmoth]

Tout d'abord, fais la distributivité.
Tu auras les termes suivants : et un terme indépendant de x.
Il te suffit de poser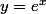 ainsi tu obtiendras une équation du second degré que tu résouds avec).

Enfin, il ne faus surtout pas oublier de reremplacer y par .
Bien sûr, il faut connaître les quelques petites règles liées au domaine des exponentielles.


Là je t'ai donné la méthode générale, qui est valable également dans les cas où tu n'as pas la factorisation du polynôme. Ici, il est vrai qu'il est plus simple de faire comme Monsieur23 a dit.

[Charlotte59]

il serait certainement plus simple de dire
(e^x +1)(e^x-4) = 0
(e^x +1) = 0 ou (e^x-4) = 0
e^x = -1 ou e^x = 4
...
en se souvent que exp :

au lieu de résoudre une équation du second degré ! enfin...