Petit probleme

par **Quidam** » 26 Oct 2006, 12:19

bastien83 a écrit:j'avais pris la fonction d'un bloc est non comme u*v

Tu as l'air de penser que "selon la méthode employée" on trouvera une dérivée différente ! C'est la négation des mathématiques !

Que tu prennes la fonction d'un bloc, ou en découpant en mille petits morceaux, ou en factorisant, ou quelle que soit la méthode, le calcul de la dérivée doit finalement arriver toujours au même résultat ! La dérivée d'un fonction ne dépend d'aucune manière de la méthode employée pour la calculer !

par **fonfon** » 26 Oct 2006, 12:30

Re,

re,

je cherche à trouver le signe de

g'(x) mais j'en suis pas tres sur:

ne s'annule pas
dc
-4x=0
x=0

c'est exacte?????

il faut utiliser g''(x) pour avoir les variations de g'(x)

g''(x) s'annule pour x=1/2 d'ou le tableau de variation de g'

la fonction g' admet un minimun absolu egal à 0 au point 1/2, la fct g' est donc strictement positive sur R et s'annule en 1/2.

avec ça tu en deduis les variations de g

par **Quidam** » 26 Oct 2006, 12:30

bastien83 a écrit:re,

je cherche à trouver le signe de

g'(x) mais j'en suis pas tres sur:

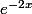
ne s'annule pas
dc
-4x=0
x=0

c'est exacte?????

Mais non !
Si

et que tu prends x=0, alors le premier terme

est effectivement égal à 0, et donc

qui n'est pas zéro !
Mais peut-être es-tu resté sur une expression fausse de g'(x) ! Ce ne serait pas étonnant, car dans ce fil on a pas mal d'opinions différentes ! Alors, j'ajoute ma propre pierre pour te confirmer que l'expression de g' donnée par fonfon est bien la bonne :

Enfin, sauf erreur :hum:

Pour savoir pour quelle(s) valeur(s) de x, la fonction g'(x) s'annulle, tu n'as pas d'autre choix que d'étudier g' en utilisant g'' !

par **bastien83** » 26 Oct 2006, 12:35

c'est une autre question

j'ai deja fais ce tableau
maintenant je dois deduire le signe de g'(x) et trouver le sens de var de g(x)

voici mon tableau si vous pouvez me confirmer

par **fonfon** » 26 Oct 2006, 12:40

non c'est faux g'(x)>0 sur R donc g est croissante on a le tableau suivant plutôt:

par **bastien83** » 26 Oct 2006, 12:47

donc le signe de g(x) sur R est +

par **fonfon** » 26 Oct 2006, 12:55

non ta fonction g est croissante sur R mais elle s'annule en x=1/2, elle est donc strictement negative sur ]-inf,1/2[ et strictement positive sur ]1/2,+inf[

Petit probleme

Qui est en ligne