Petit problème integrale et suite
21 messages
- Page 1 sur 2 - 1, 2
petit problème integrale et suite
Salut les amis
Jai un problème que voici
Soit n un nombre naturel . Considérons la fonction I_n défini sur \mathbb{R} par :
\forall x \in \mathbb{R} , I_n(x) = \bigint_{0}^{x} \frac{t^n}{n!} e^{1-t}dt
Jai réussi a prouver que
1) I_0(x) = - e-e^{1-x} et que 2) I_n(x) = I_{n-1}x - \frac{1}{(n-1)!} x^n e^{1-x}
Maintenant la question poursuit
3)Pour tout naturel non nul n
A) I_n(x) = e-1-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ]
B) I_n(x) = e-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ]
C) I_n(x) = -e+1-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ]
D) I_n(x) = 2e-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ]
4) En déduire \lim_{x \to \infty} I_n(x)
Doucement sur les explications et merci d'avance car je ne comprends vraiment pas comment une intégrale devient une suite
PS : Désolé en cas de mauvaise traduction la question est a l'origine en anglais.
Jai un problème que voici
Soit n un nombre naturel . Considérons la fonction I_n défini sur \mathbb{R} par :
\forall x \in \mathbb{R} , I_n(x) = \bigint_{0}^{x} \frac{t^n}{n!} e^{1-t}dt
Jai réussi a prouver que
1) I_0(x) = - e-e^{1-x} et que 2) I_n(x) = I_{n-1}x - \frac{1}{(n-1)!} x^n e^{1-x}
Maintenant la question poursuit
3)Pour tout naturel non nul n
A) I_n(x) = e-1-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ]
B) I_n(x) = e-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ]
C) I_n(x) = -e+1-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ]
D) I_n(x) = 2e-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ]
4) En déduire \lim_{x \to \infty} I_n(x)
Doucement sur les explications et merci d'avance car je ne comprends vraiment pas comment une intégrale devient une suite
PS : Désolé en cas de mauvaise traduction la question est a l'origine en anglais.
Re: petit problème integrale et suite
Salut les amis
Jai un problème que voici
Soit n un nombre naturel . Considérons la fonction I_n défini sur = \bigint_{0}^{x} \frac{t^n}{n!} e^{1-t}dtJai réussi a prouver que 1) I_0(x) = - e-e^{1-x} et que 2) I_n(x) = I_{n-1}x - \frac{1}{(n-1)!} x^n e^{1-x} Maintenant la question poursuit 3)Pour tout naturel non nul nA) I_n(x) = e-1-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ] B) I_n(x) = e-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ] C) I_n(x) = -e+1-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ]D) I_n(x) = 2e-e^{1-x}[1 + \bigsum_{p=1}^{n} \frac{x^p}{p!} ]4) En déduire \lim_{x \to \infty} I_n(x))
Doucement sur les explications et merci d'avance car je ne comprends vraiment pas comment une intégrale devient une suite
PS : Désolé en cas de mauvaise traduction la question est a l'origine en anglais.
Jai un problème que voici
Soit n un nombre naturel . Considérons la fonction I_n défini sur
Doucement sur les explications et merci d'avance car je ne comprends vraiment pas comment une intégrale devient une suite
PS : Désolé en cas de mauvaise traduction la question est a l'origine en anglais.
Re: petit problème integrale et suite
Peux tu modifier ton message en rajoutant les balises 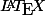 car c'est dommage.
car c'est dommage.
Re: petit problème integrale et suite
Salut les amis
Jai un problème que voici
Soit n un nombre naturel . Considérons la fonction défini sur
défini sur  par :
par :
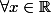 ,
, = \bigint_{0}^{x} \frac{t^n}{n!} e^{1-t}) dt
dt
Jai réussi a prouver que
1)) = - e-
= - e- et que 2)
et que 2) ) =
= 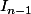 (x) -
(x) - !} x^n e^{1-x})
Maintenant la question poursuit
3)Pour tout naturel non nul n
A)) = e-1-
= e-1- [1 +
[1 + 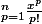 ]
]
B)) = e-
= e- [1 +
[1 + 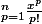 ]
]
C)) = -e+1-
= -e+1- [1 +
[1 + 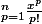 ]
]
D)) = 2e-
= 2e- [1 +
[1 + 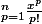 ]
]
4) En déduire (x)
(x)
Doucement sur les explications et merci d'avance car je ne comprends vraiment pas comment une intégrale devient une suite
PS : Désolé en cas de mauvaise traduction la question est a l'origine en anglais.
Jai un problème que voici
Soit n un nombre naturel . Considérons la fonction
Jai réussi a prouver que
1)
Maintenant la question poursuit
3)Pour tout naturel non nul n
A)
B)
C)
D)
4) En déduire
Doucement sur les explications et merci d'avance car je ne comprends vraiment pas comment une intégrale devient une suite
PS : Désolé en cas de mauvaise traduction la question est a l'origine en anglais.
Re: petit problème integrale et suite
Merci de ré-écrire correctement tes intégrales en utilisant la syntaxe :
I=\int_0^xf(x) dx
le tout entre balises tex, en langage LaTeX
ce qui donne :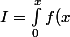 dx)
I=\int_0^xf(x) dx
le tout entre balises tex, en langage LaTeX
ce qui donne :
Re: petit problème integrale et suite
Voilà ce que j'ai compris:
 = \int_{0}^{x} \frac{t^n}{n!} e^{1-t}dt)
 = \int_{0}^{x}e^{1-t}dt=\left [-e^{1-t}\right ]_{0}^{x}=e-e^{1-x}=e\left ( 1- e^{-x}\right ))
On pose:!}) et
et 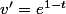
Donc: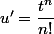 et
et 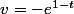
 = \int_{0}^{x} \dfrac{t^{n+1}}{(n+1)!} e^{1-t}dt=\int_{0}^{x}uv'dt=\left [ uv \right ]_{0}^{x}-\int_{0}^{x}u'vdt=\left [ -\dfrac{t^{n+1}}{(n+1)!}e^{1-t} \right ]_{0}^{x}-\int_{0}^{x}-\dfrac{t^{n}}{n!}e^{1-t}dt)
Ce qui revient à écrire:
 =I_n(x)-\dfrac{x^{n+1}}{(n+1)!}e^{1-x})
Ceci fait, dans tes explications, tu mélange énoncé et réponse donc si tu peux les séparera fin qu'on puisse t'aider ça serait bien.
On pose:
Donc:
Ce qui revient à écrire:
Ceci fait, dans tes explications, tu mélange énoncé et réponse donc si tu peux les séparera fin qu'on puisse t'aider ça serait bien.
Re: petit problème integrale et suite
Nous avons:
 =I_n(x)-\dfrac{x^{n+1}}{(n+1)!}e^{1-x}\\ I_n(x) =I_{n-1}(x)-\dfrac{x^{n}}{n!}e^{1-x}\\ \hdots\\ I_{1}(x) =I_0(x)-xe^{1-x})
Une sommation et simplification, nous permet d'écrire:
 =I_0(x)-\sum_{1}^{n+1}\dfrac{x^{k}}{k!}e^{1-x}\Rightarrow I_{n}(x) =I_0(x)-\sum_{1}^{n}\dfrac{x^{k}}{k!}e^{1-x})
 =I_0(x)-e^{1-x}\sum_{1}^{n}\dfrac{x^{k}}{k!})
Nous avons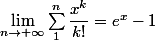
D'où :=I_0(x)-e^{1-x}(e^x-1))
Il te reste à remplacer) et simplifier
et simplifier
Une sommation et simplification, nous permet d'écrire:
Nous avons
D'où :
Il te reste à remplacer
Re: petit problème integrale et suite
Razes a écrit:Nous avons:
Une sommation et simplification, nous permet d'écrire:
Nous avons
D'où :
Il te reste à remplaceret simplifier
pourquoi
merci
Re: petit problème integrale et suite
en fait je viens de comprendre ce que tu voulais dire par sommation et simplification du coup j'ai pu terminer l'exercice grand merci Razès ça faisais déjà 1mois que j'étais sur ce problème
Re: petit problème integrale et suite
Je suis heureux pour toi.

J'espère que tu n'as pas tiré en l'air?focon a écrit:en fait je viens de comprendre ce que tu voulais dire par sommation et simplification du coup j'ai pu terminer l'exercice grand merci Razès ça faisais déjà 1mois que j'étais sur ce problème

Re: petit problème integrale et suite
MDR en fait non mais si j'avais pu je l'aurait fait
Modifié en dernier par focon le 10 Sep 2016, 15:42, modifié 1 fois.
Re: petit problème integrale et suite
Razes a écrit:1) Ne serait ce pas plutôt?
et pour ça tu avais raison cool il y a un "-" que j'avais oublié
Re: petit problème integrale et suite
Depuis le 5 tu viens juste de le voir? A quoi ça sert que Ducros se décarcasse?
Re: petit problème integrale et suite
MDR désolé
mais n'exagère pas non-plus c'était le 08 et non le 05
mais n'exagère pas non-plus c'était le 08 et non le 05
Re: petit problème integrale et suite
Ce n'est pas grave. Mais ce n'est ni le 8 ni le 4 mais le 5 (revois le message).
Bon courage
Bon courage
Re: petit problème integrale et suite
ah tu parles de ) je l'avais vu mais il fallait que je comprenne comment procéder pour prendre ça en compte non??
je l'avais vu mais il fallait que je comprenne comment procéder pour prendre ça en compte non??
Re: petit problème integrale et suite
Non, de ce message.
Messagepar Razes » 05 Sep 2016 07:37
Messagepar Razes » 05 Sep 2016 07:37
Razes a écrit:1) Ne serait ce pas plutôt?
Re: petit problème integrale et suite
OK en tout cas merci je pense que vous pouvez envoyer le sujet a la corbeille
Modifié en dernier par focon le 10 Sep 2016, 19:36, modifié 1 fois.
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
