Un petit devoir maison sur les formules de cardan

[Hick_Jeck]

Bonjour à tous,
Notre prof de maths nous propose à l'occasion d'un DM l'élaboration d'une méthode permettant la résolution d'équations du troisième degré de ce type : .

Pour cela, on doit tout d'abord (d'après l'énoncé) considérer deux nombres u et v tels que :


Dans la première question, il s'agit ici de montrer que est solution de l'équation .

C'est malheureusement dès cette question que je bloque. J'ai pensé à utiliser un tableau de variation de en fonction des valeurs de p et de q, mais ça me semble tendu et ce serait beaucoup d'efforts pour une issue incertaine, d'autant que je n'ai pas d'expression exacte de u et de v.

J'ai jusqu'à vendredi, donc rien n'est vraiment encore urgent.

En vous remerciant par avance de m'aiguiller (et non de me donner la solution ),
Amicalement,
Hick_Jeck

[Nightmare]

Salut !

On te demande de montrer u+v est solution de x^3+px+q=0, ce qui revient simplement à montrer que (u+v)^3+p(u+v)+q=0

Je te laisse essayer

[Hick_Jeck]

Salut !

On te demande de montrer u+v est solution de x^3+px+q=0, ce qui revient simplement à montrer que (u+v)^3+p(u+v)+q=0

Je te laisse essayer

Je suis bête :/ . Je devrais éviter le maths après une journée fatigante . Je cherche vraiment trop compliqué.

On a donc

Donc u+v est bien solution de l'équation

[Nightmare]

Niquel :happy3:

[Hick_Jeck]

Merci .

2) Il s'agit alors de montrer (par substitution) que et sont solutions de l'équation .

Dans le doute de ce que représente X :/ . De plus, la substitution est-elle à appliquer au système mettant en jeu u et v ou autre chose ? Une piste ? :we:

Je viens de commencer à chercher la question, donc soyez vagues :we: .

En vous remerciant encore,
Amicalement,
Hick_Jeck.

[Nightmare]

Je note U=u^3 et V=v^3

On sait déjà que U+V=-q et UV=(uv)^3=-p^3/27

Effectue ensuite, comme tu l'as intuité, une substitution :happy3:

[Hick_Jeck]

Han wé . Merci. D'après ce que t'as dit :


D'où et

Avant d'aller plus loin, est-ce que je pars sur une bonne piste ? Ça me parait relativement incohérent...

[Hick_Jeck]

Mmh. En fait, je pense que ma démarche est fausse quelque part puisque je suis censé sortir « X » de ma factorisation et en plus avoir une expression du type « 1/X » au sein de ma factorisation... Pourtant, le raisonnement parait répondre à la question :/ .

[Nightmare]

C'est exactement la même chose que ta première question, je croyais que tu avais compris !

[mathelot]

Donc u+v est bien solution de l'équation


Pas vraiment. Le raisonnement est plutôt du type:

si l'on trouve une racine à ce polynome de degré 3,
c'est gagné car on a la possibilité (théorique) de le factoriser

On cherche cette racine sous la forme x=u+v
et l'on s'aperçoit que l'on peut obtenir une racine x de la forme u+v
si et sont solutions d'une équation du second degré.

Dans la méthode de Cardan, on cherche surtout une formule d'algèbre
et non pas d'analyse. En effet l'analyse nous donne de nombreuses certitudes

i) les polynomes de degré 3 ont une racine réelle (TVI)

ii) je crois me rappeler que cette racine est située
dans l'intervalle [-R;R] où R=max(|a|+|b|+|c|+|d|,1)
où a,b,c,d sont les coeff du polynome

iii) la suite récurrente
donne des valeurs approchées d'une racine.

[Hick_Jeck]

Me voilà donc un peu plus en forme...

-------------




On note et .
Pour , on a :



De même, pour , on a :


On a donc bien montré que et étaient solution de l'équation .

--------------

Est-ce correct d'un point de vue rédactionnel, d'un point de vue mathématique ?

Merci d'avance, après, je passe à la troisième question.

[Hick_Jeck]

Mmh, avant de vous laisser le temps de vérifier, j'ai un peu regardé la troisième question et je suis un peu à cours d'idées là (comme d'habitude :hein: ).

« En déduire que et sont solutions de l'équation du deuxième degré ».

Je passe par un calcul de discriminant ? Ça me semble une alternative compliquée. La méthode de poser X = et X = ne paraît pas applicable directement ici, me trompe-je ?

[Clu]

Ne cherche pas compliqué ici c'est très simple.
Sans considérer u^3 et v^3, en oubliant les solutions de l'équation, essaie de passer de la 1ère équation à la 2e...(désolé si j'avais pas envie de les réécrire). Il s'agit ici d'un simple raisonnement par équivalence (u^3 et v^3 n'ont rien à voir là dedans). N'oublie pas que tu peux ajouter ou multiplier par un même nombre les deux membres d'une équation.

[Hick_Jeck]

Ne cherche pas compliqué ici c'est très simple.
Sans considérer u^3 et v^3, en oubliant les solutions de l'équation, essaie de passer de la 1ère équation à la 2e...(désolé si j'avais pas envie de les réécrire). Il s'agit ici d'un simple raisonnement par équivalence (u^3 et v^3 n'ont rien à voir là dedans). N'oublie pas que tu peux ajouter ou multiplier par un même nombre les deux membres d'une équation.

Merci bien.


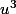
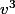
Voilà. Comment je peux en conclure que et sont solutions ? Intuitivement, c'est évident, maintenant, au niveau de la rédaction, est-ce que ça passe aussi si je dis simplement que je peux remplacer X par U et V ?

Bon, sans plus tarder, je vais passer à la suite, j'ai une fin de semaine assez chargée.

« Mise en œuvre de la méthode sur un exemple
On considère l'équation et on cherche une solution sous la forme u+v selon la méthode précédente.
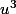
1) Déterminer l'équation du deuxième degré vérifiée par et .
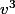
2) En déduire les valeurs de u et v.
3) En déduire une solution de l'équation . Existe-t-il une autre solution dans ? »

1) D'après la méthode générale, l'équation peut-être du type .

2) Ici, on a et , d'où :

-1 est une racine évidente, on a donc une factorisation de la forme :

(une erreur s'est glissée lors de la factorisation. X-8 = 0 bien entendu.)

D'où et . Donc et

3) est solution de l'équation.
Pour vérifier si il n'y a pas d'autres solutions, je factorise et je vois si ça fonctionne :

et x est unique car x^2+7x = 0 n'a pas de solution dans R (delta < 0).

Tout est ok ?

Je transmets les trois autres équations et finis le DM si possible ce soir.

[Hick_Jeck]

Bon, j'ai deux autres équations à résoudre qui me paraissent du même type (si j'ai des problèmes dessus, je poste ici). Le dernier paraît un peu plus tendu en revanche :
« Résoudre l'équation : (utiliser le changement de variable .) ».

Je suppose qu'il faut poser puis :

C'est la même méthode alors. À la calculette : ou . D'où et , et .


u+v est solution. Cela dit, la factorisation reste assez complexe. Y'a-t-il moyen de simplifier le bélude pour prouver, comme je le vois sur la courbe, qu'il n'y a qu'une seule solution ? (TVI ?)

Une fois que c'est démontré, on a . D'où, .

Voilà voilà.

[Hick_Jeck]

Désolé, c'est facile à démontrer avec le TVI. Si quelqu'un pouvait passer un peu de temps sur la méthode générale et le mise en œuvre de la méthode sur un exemple, pour voir si ma rédaction est à peu près correcte ?

En vous remerciant par avance,
Hick_Jeck