Un petit/bon exercice sur les nombres complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 31 Jan 2019, 14:20
par zerow2001 » 31 Jan 2019, 14:20
Avant tous, Salut

Z et T sont deux nombres complexes et :
On sait que :
|Z| ≥ 1
|T| ≥ 1
|Z+T| < 1
-Montrez que |Z² + T²| ≥ 1
Et Merci d'vance


-
aviateur
 par aviateur » 31 Jan 2019, 14:53
par aviateur » 31 Jan 2019, 14:53
Bonjour
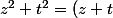^2-2 z t)
d'où

cqfd
Modifié en dernier par aviateur le 31 Jan 2019, 17:32, modifié 1 fois.
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 31 Jan 2019, 15:00
par zerow2001 » 31 Jan 2019, 15:00
aviateur a écrit:Bonjour
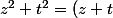^2-2 z t)
d'où
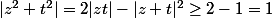
cqfd
peux-tu detailler un peu svp ?
-
aviateur
 par aviateur » 31 Jan 2019, 15:38
par aviateur » 31 Jan 2019, 15:38
J'ai utilisé l'inégalité triangulaire et les hypothèses.... j'ai corrigé
Modifié en dernier par aviateur le 31 Jan 2019, 17:37, modifié 1 fois.
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 31 Jan 2019, 15:45
par zerow2001 » 31 Jan 2019, 15:45
aviateur a écrit:Quel détail? J'ai utilisé l'inégalité triangulaire et les hypothèses, c'est tout.
J'ai pas commpris comment tu as trouver le |Z²+T²| dans la derniere égalité
-
aviateur
 par aviateur » 31 Jan 2019, 17:36
par aviateur » 31 Jan 2019, 17:36
Non c'est une erreur de frappe c'est supérieur ou égal. (j'ai utlisé l'inégalité triangulaire. Je comprends pourquoi tu n'avait pas compris. J'ai donc corrigé.
L'inégalité triangulaire c'est

| donc

ou alors

ça va comme ça?
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 31 Jan 2019, 20:06
par zerow2001 » 31 Jan 2019, 20:06
aviateur a écrit:Non c'est une erreur de frappe c'est supérieur ou égal. (j'ai utlisé l'inégalité triangulaire. Je comprends pourquoi tu n'avait pas compris. J'ai donc corrigé.
L'inégalité triangulaire c'est

| donc

ou alors

ça va comme ça?
Est-ce que t'as corrigé la premiere réponse ?
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 31 Jan 2019, 20:13
par zerow2001 » 31 Jan 2019, 20:13
J'ai pas compris pourquoi : |z²+t²| > 2|zt|-|z+t|²
-
aviateur
 par aviateur » 31 Jan 2019, 20:18
par aviateur » 31 Jan 2019, 20:18
C'est l'inégalité triangulaire avec a=-2zt et b=(z+t)^2
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 31 Jan 2019, 20:28
par zerow2001 » 31 Jan 2019, 20:28
comme tu as dis on va avoir :
|-2zt + (z+t)²| < |-2zt|+|(z+t)²| alors : |z²+t²| < 2|zt|+|(z+t)²|
-
aviateur
 par aviateur » 31 Jan 2019, 21:18
par aviateur » 31 Jan 2019, 21:18
Bonjour
Si tu prends l'inégalité triangulaire dans le sens usuel cela sera peut être plus facile:
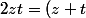^2-(z^2+t^2))
dc

i.e

-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 31 Jan 2019, 21:44
par zerow2001 » 31 Jan 2019, 21:44
J'ai compris merci beaucoup aviateur <3
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 31 Jan 2019, 21:52
par zerow2001 » 31 Jan 2019, 21:52
S'il vous plait aviateur, j'ai un trés bon sujet sur les nombres complexes, si vous avez de temps de me repondre ?
-
aviateur
 par aviateur » 31 Jan 2019, 22:13
par aviateur » 31 Jan 2019, 22:13
Tu peux toujours essayer. De toute façon je ne suis pas seul sur le forum
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 31 Jan 2019, 22:15
par zerow2001 » 31 Jan 2019, 22:15
aviateur a écrit:Tu peux toujours essayer. De toute façon je ne suis pas seul sur le forum
Oui, je ne pose pas un sujet sans essayer, toujours.
mais si tu veux m'aide, ca va etre tres gentil
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
d'où
cqfd
| donc
ou alors