Bonjour à toutes et tous.
Dans le temps (quand j'étais en terminale), nous avions vu en maths comment résoudre une équation du type z4-1=0 (il s'agit de nombres imaginaires, donc) par la méthode des approximations de Newton.
J'essaie de retrouver cette méthode, mais il n'y a plus rien, en tous les cas, dans ma mémoire ;-)
Est-ce que quelqu'un peut me rafraîchir ?? (euh, mes années lycées sont bien lointaines, et j'ai tout perdu du peu de maths que je comprenais alors... Merci d'être soft, techniquement parlant, dans vos réponses :briques:
Daniel B.
Z4-1=0 par la méthode de Newton
6 messages
- Page 1 sur 1
par N_comme_Nul » 09 Aoû 2005, 19:23
Salut !
Ici, pas besoin d'approximations ... on peut connaître les valeurs exactes.
Tu (je peux ?) peux trouver des racines évidentes :
et -1 en sont, tu peux donc factoriser par (z+1))
.
Les deux autres racines sont complexes.
Quand on factorise on arrive à(z+1)(z^2+1))
et ce dernier facteur, on sait le factoriser : (z+i))
.
Ici, pas besoin d'approximations ... on peut connaître les valeurs exactes.
Tu (je peux ?) peux trouver des racines évidentes :
Les deux autres racines sont complexes.
Quand on factorise on arrive à
par dbourrion » 10 Aoû 2005, 06:09
N_comme_Nul a écrit:Salut !
Ici, pas besoin d'approximations ... on peut connaître les valeurs exactes.
Certes mais ce qui m'intéresse ici, ce ne sont pas les valeurs (que je connais), mais la méthode : c'est sur elle que je veux remettre la main :id:
par Anonyme » 10 Aoû 2005, 08:59
bonjour,
c'est la méthode des tangentes classique qu'on peut étendre à la résolution d'un système:
=0)
=0)
ici la relation de recurrence est:
=\(<br />\begin{array}<br /> x_{n} \\<br /> y_{n} \\<br /> \end{array}<br />\)-J^{-1}*\(<br />\begin{array}<br /> f(x_{n},y_{n}) \\<br /> g(x_{n},y_{n}) \\<br /> \end{array}<br />\))
où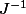
est l'inverse de la matrice jacobienne évaluée au point )
la jacobienne J étant:
<br />\] & \[<br />\frac{\partial }{{\partial y}}f(x,y)<br />\] \\<br /> \[<br />\frac{\partial }{{\partial x}}g(x,y)<br />\] & \[<br />\frac{\partial }{{\partial y}}g(x,y)<br />\] \\<br /> \end{array}<br />\))
z^4-1=0
équivaut à (avec z=x+iy):
=x^4-6x^2y^2+y^4-1=0)
=4x^3y-4xy^3=0)
donc concrètement, tu pars d'une valeur initiale (x0,y0) que tu fais tourner dans la moulinette et en principe tu tomberas sur les solutions...
j'ai pas testé.
remarque:
la méthode simple de newton ne te donneras pas les valeurs cplx, voila pourquoi il faut passer à un système à résoudre ...si tu veux les avoir.
c'est la méthode des tangentes classique qu'on peut étendre à la résolution d'un système:
ici la relation de recurrence est:
où
la jacobienne J étant:
z^4-1=0
équivaut à (avec z=x+iy):
donc concrètement, tu pars d'une valeur initiale (x0,y0) que tu fais tourner dans la moulinette et en principe tu tomberas sur les solutions...
j'ai pas testé.
remarque:
la méthode simple de newton ne te donneras pas les valeurs cplx, voila pourquoi il faut passer à un système à résoudre ...si tu veux les avoir.
par dbourrion » 10 Aoû 2005, 17:51
12h33 a écrit:bonjour,
z^4-1=0
équivaut à (avec z=x+iy):
donc concrètement, tu pars d'une valeur initiale (x0,y0) que tu fais tourner dans la moulinette et en principe tu tomberas sur les solutions...
.
J'ai pas tout compris (c'est un euphémisme....) mais la fin me parle un peu et, oh miracle, me rappelle vaguement quelque chose.
Merci.
par Anonyme » 11 Aoû 2005, 09:19
Pour résoudre f(x)=0 : méthode des tangentes (newton)
(on suppose que f est dérivable sur un intervalle I et s'annule en
, f monotone sur I)
Par exemple: on veut résoudre=e^x-x/7-2=0)
on peut voir que f s'annule en x#0.7
partons de x=2
tracons la tangente à Cf en x0=2
la tangente coupe l'axe Ox en x1
tracons la tangente à Cf en x1
elle coupe Ox en x2
...
etc..
on crée une suite :
} {f'(x_n)})
qui (dans notre cas) va tendre vers
voila le principe.
dans le cas de
cette méthode fournira la ou les solutions réelles de l'équation.
pas les cplx.
pour obtenir les solutions cplx, on pose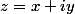
alors
devient
+i(4x^3y-4xy^3)=0)
qui est equiv à
système à résoudre, donc.
mais la méthode généralisée ne se fait pas en term puisqu'elle fait appel à la matrice jacobienne...
mais j'ai donné la formulee ds un post précédent.
voilà.
(on suppose que f est dérivable sur un intervalle I et s'annule en
Par exemple: on veut résoudre
on peut voir que f s'annule en x#0.7
partons de x=2
tracons la tangente à Cf en x0=2
la tangente coupe l'axe Ox en x1
tracons la tangente à Cf en x1
elle coupe Ox en x2
...
etc..
on crée une suite :
qui (dans notre cas) va tendre vers
voila le principe.
dans le cas de
cette méthode fournira la ou les solutions réelles de l'équation.
pas les cplx.
pour obtenir les solutions cplx, on pose
alors
devient
qui est equiv à
système à résoudre, donc.
mais la méthode généralisée ne se fait pas en term puisqu'elle fait appel à la matrice jacobienne...
mais j'ai donné la formulee ds un post précédent.
voilà.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :